Uniformly separate several subsets from a given set

This is a demo to uniformly separate two subsets from a given set by using Mixed Integer Linear Programming (MILP). It reproduces the experiment in the paper.

Reference:

1. "Single- and Multiple-Shell Uniform Sampling Schemes for Diffusion MRI Using Spherical Codes", Jian Cheng, Dinggang Shen, Pew-Thian Yap, Peter J. Basser, IEEE Transactions on Medical Imaging, 2017.

2. "Designing Single- and Multiple-Shell Sampling Schemes for Diffusion MRI Using Spherical Code", Jian Cheng, Dinggang Shen, Pew-Thian Yap, MICCAI 2014.

Copyright (c) 2013, Jian Cheng (jian.cheng.1983@gmail.com)

Contents

Read two sets of uniform directions

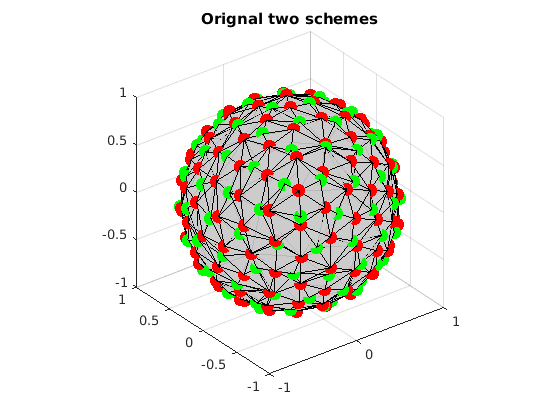
grad1 = ReadDirections([getenv('HOME'), '/.dmritool/Data/Tessellation/directions_t3.txt']);
n1 = size(grad1, 1);

grad2 = ReadDirections([getenv('HOME'), '/.dmritool/Data/ElectricRepulsion/Elec060.txt']);
n2 = size(grad2, 1);

% Visualize the original two schemes. Different colors denote samples in different shells.
VisualizeMultiShellScheme(grad1, grad2);
title(['Orignal two schemes']);

Randomly mix these two sets

index = randperm(n1+n2);

gradAll = [grad1; grad2];
gradAll = gradAll(index,:);

% Visualize the mixed two schemes.
VisualizeMultiShellScheme(gradAll);
title(['Randomly mixed scheme']);

Extract two sets using MILP

Now we want to seperate these two sets from the mixture.

clear params grbParams
% set parameters
% w=1 means we do not care about the combined shell with all samples. See the paper.
params.w=1;
params.numSamples=[n1 n2];

% use default grb parameters
[gradCell, grb, indexMatrix]=OptimalSamplingMultiSubsetsFromSameSet(gradAll,params, []);

MIPFocus = 1
Academic license - for non-commercial use only
Optimize a model with 1105 rows, 285 columns and 3855 nonzeros
Model has 141 SOS constraints
Variable types: 3 continuous, 282 integer (282 binary)
Coefficient statistics:
  Matrix range     [1e+00, 2e+00]
  Objective range  [5e-01, 5e-01]
  Bounds range     [3e-02, 1e+00]
  RHS range        [3e+00, 8e+01]
Presolve added 9 rows and 0 columns
Presolve removed 0 rows and 1 columns
Presolve time: 0.02s
Presolved: 1114 rows, 284 columns, 3477 nonzeros
Variable types: 2 continuous, 282 integer (282 binary)
Found heuristic solution: objective 0.0409562
Found heuristic solution: objective 0.0816685

Root relaxation: objective 3.139177e-01, 632 iterations, 0.01 seconds

    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time

     0     0    0.31392    0  282    0.08167    0.31392   284%     -    0s
H    0     0                       0.2978894    0.31392  5.38%     -    0s
H    0     0                       0.2978896    0.31392  5.38%     -    0s
     0     0     cutoff    0         0.29789    0.29789  0.00%     -    0s

Cutting planes:
  Clique: 60
  MIR: 2
  StrongCG: 155
  Zero half: 1

Explored 1 nodes (933 simplex iterations) in 0.16 seconds
Thread count was 8 (of 8 available processors)

Solution count 4: 0.29789 0.297889 0.0816685 0.0409562 

Optimal solution found (tolerance 1.00e-04)
Best objective 2.978895564717e-01, best bound 2.978895564717e-01, gap 0.0000%

Test the results

covering radius comparison

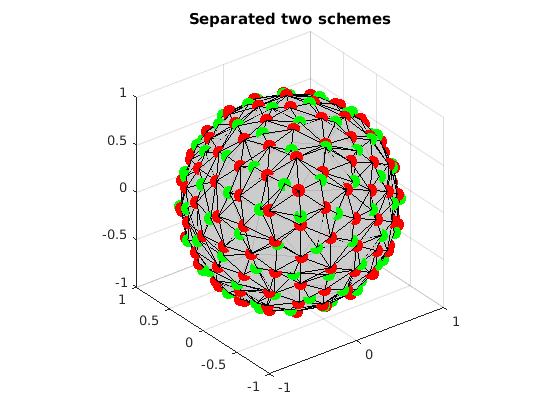
fprintf('covering radius of set 1 = %f degree\n', CoveringRadius(grad1)*180/pi);
fprintf('covering radius of set 2 = %f degree\n', CoveringRadius(grad2)*180/pi);
fprintf('covering radius of extracted set 1 = %f degree\n', CoveringRadius(gradCell{1})*180/pi);
fprintf('covering radius of extracted set 2 = %f degree\n', CoveringRadius(gradCell{2})*180/pi);

% number of wrongly detected samples
fprintf('the number of extracted directions not in set 1: %d\n', n1-sum(indexMatrix(index<=n1,1)))
fprintf('the number of extracted directions not in set 2: %d\n', n2-sum(indexMatrix(index>n1,2)))

% Visualize the separated two sets
VisualizeMultiShellScheme(gradCell{1}, gradCell{2});
title(['Separated two schemes']);

covering radius of set 1 = 15.858714 degree
covering radius of set 2 = 18.276892 degree
covering radius of extracted set 1 = 15.858714 degree
covering radius of extracted set 2 = 18.276892 degree
the number of extracted directions not in set 1: 0
the number of extracted directions not in set 2: 0

Published with MATLAB® R2015b