#include <itkSphericalHarmonicsGenerator.h>

Inheritance diagram for itk::SphericalHarmonicsGenerator< PreciseType >:

Collaboration diagram for itk::SphericalHarmonicsGenerator< PreciseType >:

Detailed Description

template<class PreciseType = double>
class itk::SphericalHarmonicsGenerator< PreciseType >

Generate complex and real Spherical Harmonic Basis.

The complex Spherical Harmonic basis is defined as

$y_l^m = \sqrt{\frac{2l+1}{4\pi}\frac{(l-m)!}{(l+m)!}} e^{im\phi} P_l^m(\cos\theta)$

The real SH basis is defined as

$Y_l^m(\theta,\phi) = \left\{ \begin{array}{lcl} \sqrt{2}\mbox{Re}(y_l^{|m|}(\theta,\phi)) = \sqrt{2}(-1)^m\mbox{Re}(y_l^m(\theta,\phi)) & \mbox{if} & -l\leq m<0 \\ y_l^m(\theta,\phi) & \mbox{if} & m=0 \\ \sqrt{2}\mbox{Im}(y_l^m(\theta,\phi)) & \mbox{if} & l\geq m>0 \end{array}\right.$

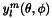where $y_l^m(\theta,\phi)$ is the complex SH basis

Author: Jian Cheng

Definition at line 54 of file itkSphericalHarmonicsGenerator.h.

Public Types
typedef SmartPointer< const Self >	ConstPointer

typedef SmartPointer< Self >	Pointer

typedef SphericalHarmonicsGenerator	Self

typedef Object	Superclass

Public Member Functions
virtual ::itk::LightObject::Pointer	CreateAnother (void) const

virtual const char *	GetNameOfClass () const

Static Public Member Functions
static std::complex< double >	ComplexDerivativeOfPhi (const int l, const int m, const double theta, const double phi)

static std::complex< double >	ComplexDerivativeOfTheta (const int l, const int m, const double theta, const double phi)

static std::complex< PreciseType >	ComplexSH (const int l, const int m, const PreciseType theta, const PreciseType phi)

static PreciseType	ComplexTripleIntegration (const int l1, const int m1, const int l2, const int m2, const int l3, const int m3)

static Pointer	New ()

static double	RealDerivativeOfPhi (const int l, const int m, const double theta, const double phi)

static double	RealDerivativeOfTheta (const int l, const int m, const double theta, const double phi)

static PreciseType	RealSH (const int l, const int m, const PreciseType theta, const PreciseType phi)

static PreciseType	RealTripleIntegration (const int l1, const int m1, const int l2, const int m2, const int l3, const int m3, const bool is_precalculated=true)

Protected Member Functions
void	PrintSelf (std::ostream &os, Indent indent) const ITK_OVERRIDE

	SphericalHarmonicsGenerator ()

virtual	~SphericalHarmonicsGenerator ()

Private Member Functions
void	operator= (const Self &)

	SphericalHarmonicsGenerator (const Self &)

Member Typedef Documentation

template<class PreciseType = double>

typedef SmartPointer<const Self> itk::SphericalHarmonicsGenerator< PreciseType >::ConstPointer

Definition at line 61 of file itkSphericalHarmonicsGenerator.h.

template<class PreciseType = double>

typedef SmartPointer<Self> itk::SphericalHarmonicsGenerator< PreciseType >::Pointer

Definition at line 60 of file itkSphericalHarmonicsGenerator.h.

template<class PreciseType = double>

typedef SphericalHarmonicsGenerator itk::SphericalHarmonicsGenerator< PreciseType >::Self

Standard class typedefs.

Definition at line 58 of file itkSphericalHarmonicsGenerator.h.

template<class PreciseType = double>

typedef Object itk::SphericalHarmonicsGenerator< PreciseType >::Superclass

Definition at line 59 of file itkSphericalHarmonicsGenerator.h.

Constructor & Destructor Documentation

template<class PreciseType >

itk::SphericalHarmonicsGenerator< PreciseType >::SphericalHarmonicsGenerator ( )

protected

Definition at line 43 of file itkSphericalHarmonicsGenerator.hxx.

template<class PreciseType >

itk::SphericalHarmonicsGenerator< PreciseType >::~SphericalHarmonicsGenerator ( )

protectedvirtual

Definition at line 49 of file itkSphericalHarmonicsGenerator.hxx.

template<class PreciseType = double>

itk::SphericalHarmonicsGenerator< PreciseType >::SphericalHarmonicsGenerator ( const Self & )

private

Member Function Documentation

template<class PreciseType >

std::complex< double > itk::SphericalHarmonicsGenerator< PreciseType >::ComplexDerivativeOfPhi	(	const int	l,
		const int	m,
		const double	theta,
		const double	phi
	)

static

get value of the derivative of phi for Complex SH basis

Definition at line 231 of file itkSphericalHarmonicsGenerator.hxx.

template<class PreciseType >

std::complex< double > itk::SphericalHarmonicsGenerator< PreciseType >::ComplexDerivativeOfTheta	(	const int	l,
		const int	m,
		const double	theta,
		const double	phi
	)

static

get value of the derivative of theta for Complex SH basis

Definition at line 216 of file itkSphericalHarmonicsGenerator.hxx.

References spams::abs(), and utl::Gamma().

Here is the call graph for this function:

template<class PreciseType >

std::complex< PreciseType > itk::SphericalHarmonicsGenerator< PreciseType >::ComplexSH	(	const int	l,
		const int	m,
		const PreciseType	theta,
		const PreciseType	phi
	)

static

get value of Complex SH basis

Definition at line 64 of file itkSphericalHarmonicsGenerator.hxx.

References utl::IsEven(), and utl::sign().

Here is the call graph for this function:

template<class PreciseType >

PreciseType itk::SphericalHarmonicsGenerator< PreciseType >::ComplexTripleIntegration	(	const int	l1,
		const int	m1,
		const int	l2,
		const int	m2,
		const int	l3,
		const int	m3
	)

static

get value of the triple integral of Complex SH basis

Definition at line 109 of file itkSphericalHarmonicsGenerator.hxx.

References spams::abs(), M_PI, and utlException.

Here is the call graph for this function:

template<class PreciseType = double>

virtual::itk::LightObject::Pointer itk::SphericalHarmonicsGenerator< PreciseType >::CreateAnother ( void ) const

template<class PreciseType = double>

virtual const char* itk::SphericalHarmonicsGenerator< PreciseType >::GetNameOfClass ( ) const

virtual

Standard part of every itk Object.

template<class PreciseType = double>

static Pointer itk::SphericalHarmonicsGenerator< PreciseType >::New ( )

static

Method for creation through the object factory.

template<class PreciseType = double>

void itk::SphericalHarmonicsGenerator< PreciseType >::operator= ( const Self & )

private

template<class PreciseType >

void itk::SphericalHarmonicsGenerator< PreciseType >::PrintSelf	(	std::ostream &	os,
		Indent	indent
	)		const

protected

Definition at line 56 of file itkSphericalHarmonicsGenerator.hxx.

template<class PreciseType >

double itk::SphericalHarmonicsGenerator< PreciseType >::RealDerivativeOfPhi	(	const int	l,
		const int	m,
		const double	theta,
		const double	phi
	)

static

get value of the derivative of phi for Real SH basis

Definition at line 254 of file itkSphericalHarmonicsGenerator.hxx.

References utl::SQRT2.

template<class PreciseType >

double itk::SphericalHarmonicsGenerator< PreciseType >::RealDerivativeOfTheta	(	const int	l,
		const int	m,
		const double	theta,
		const double	phi
	)

static

get value of the derivative of theta for Real SH basis

Definition at line 241 of file itkSphericalHarmonicsGenerator.hxx.

References utl::SQRT2.

template<class PreciseType >

PreciseType itk::SphericalHarmonicsGenerator< PreciseType >::RealSH	(	const int	l,
		const int	m,
		const PreciseType	theta,
		const PreciseType	phi
	)

static

get value of Real SH basis

Definition at line 83 of file itkSphericalHarmonicsGenerator.hxx.

References utl::IsEven(), utl::sign(), and utl::SQRT2.

Referenced by utl::ComputeDWISHCoefficientsForGPDCylinder(), itk::SphericalPolarFourierGenerator< PreciseType >::Evaluate(), utl::GetSymmetricTensorSHCoef(), and utl::GetSymmetricTensorSHCoefDerivative().

Here is the call graph for this function:

Here is the caller graph for this function:

template<class PreciseType >

PreciseType itk::SphericalHarmonicsGenerator< PreciseType >::RealTripleIntegration	(	const int	l1,
		const int	m1,
		const int	l2,
		const int	m2,
		const int	l3,
		const int	m3,
		const bool	is_precalculated = `true`
	)