Collaboration diagram for UtlMath:

Namespaces
	utl

	utl::Functor

Macros
#define	__utl_geev_Matrix(T, FuncName, RowMajorMatrixName, GetRowsFuncName, GetColsFuncName, MatrixGetDataFuncName, VectorName, VectorGetDataFuncName, ReSizeFuncName)

#define	__utl_gemm_MatrixTimesMatrix(T, FuncName, FuncHelperName, RowMajorMatrixName, GetRowsFuncName, GetColsFuncName, GetDataFuncName, ReSizeFuncName)

#define	__utl_gemv_MatrixTimesVector(T, FuncName, FuncHelperName, RowMajorMatrixName, GetRowsFuncName, GetColsFuncName, MatrixGetDataFuncName, VectorName, GetSizeFuncName, VectorGetDataFuncName, ReSizeFuncName)

#define	__utl_getri_Matrix(T, FuncName, RowMajorMatrixName, GetRowsFuncName, GetColsFuncName, MatrixGetDataFuncName, ReSizeFuncName)

#define	__utl_gevm_MatrixTimesVector(T, FuncName, FuncHelperName, RowMajorMatrixName, GetRowsFuncName, GetColsFuncName, MatrixGetDataFuncName, VectorName, GetSizeFuncName, VectorGetDataFuncName, ReSizeFuncName)

#define	__utl_syrk_Matrix(T, FuncName, FuncHelperName, RowMajorMatrixName, GetRowsFuncName, GetColsFuncName, GetDataFuncName, ReSizeFuncName)

#define	lapack_complex_double std::complex<double>

#define	lapack_complex_float std::complex<float>

Typedefs
typedef double(*	utl::Func1To1) (double)

Functions
template<class ExprT >
auto	utl::Abs (const ExprT &expr) -> decltype(utl::F< utl::Functor::Abs< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::Acos (const ExprT &expr) -> decltype(utl::F< utl::Functor::Acos< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::Asin (const ExprT &expr) -> decltype(utl::F< utl::Functor::Asin< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::Atan (const ExprT &expr) -> decltype(utl::F< utl::Functor::Atan< typename ExprT::ValueType > >(expr))

template<class TLeft >
auto	utl::Atan2 (const TLeft &lhs, const ScalarExpr &rhs) -> decltype(utl::F< utl::Functor::Atan2< Expr2ValueType< TLeft, ScalarExpr >> >(lhs, rhs))

template<class TRight >
auto	utl::Atan2 (const ScalarExpr &lhs, const TRight &rhs) -> decltype(utl::F< utl::Functor::Atan2< Expr2ValueType< ScalarExpr, TRight >> >(lhs, rhs))

template<class TLeft , class TRight >
auto	utl::Atan2 (const TLeft &lhs, const TRight &rhs) -> decltype(utl::F< utl::Functor::Atan2< Expr2ValueType< TLeft, TRight >> >(lhs, rhs))

double	utl::BesselJa (const double a, const double x)

double	utl::BesselJInteger (const int n, const double x)

double	utl::BesselJIntegerPrime (const int n, const double x)

template<typename T >
T	utl::Binomial (const T v1, const int times)

template<class T >
utl_shared_ptr< utl::NDArray< T, 1 > >	utl::ComputeDWISHCoefficientsForGPDCylinder (const T radius, const T diffusivity, const T deltaBig, const T deltaSmall, const T qq, const int lMax, const T theta=0, const T phi=0)

template<class T >
double	utl::ComputeOrientationalOrderFromSHCoefficients (const utl::NDArray< T, 1 > &shCoef, const utl::NDArray< T, 1 > &axis)

double	utl::ComputeOrientationalOrderFromSymmetricTensor (const double e1, const double e2, const double phi=0)

template<class ExprT >
auto	utl::Conj (const ExprT &expr) -> decltype(utl::F< utl::Functor::Conj< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::Cos (const ExprT &expr) -> decltype(utl::F< utl::Functor::Cos< typename ExprT::ValueType > >(expr))

template<class TVector1 , class TVector2 , class TVector3 >
double	utl::CrossProduct (const TVector1 &v1, const TVector2 &v2, TVector3 &v3)

template<class ExprT >
auto	utl::Cube (const ExprT &expr) -> decltype(utl::F< utl::Functor::Cube< typename ExprT::ValueType > >(expr))

double	utl::DawsonF (double x)

template<class TMatrixType >
auto	utl::DeterminantSmallMatrix (const TMatrixType &mat, const int row) -> utl::remove_reference_t< decltype(mat(0, 0))>

template<class TVector1 , class TVector2 >
double	utl::DotProduct (const TVector1 &v1, const TVector2 &v2, const int N1)

template<class T >
void	utl::EigenDecompositionSymmetricVnlMatrix (const vnl_matrix< T > &mat, vnl_vector< T > &eigenValues, vnl_matrix< T > &eigenVectors)

template<class VectorType >
double	utl::Entropy (const VectorType &pdfVec, const int N)

double	utl::Erf (double x)

double	utl::Erfi (double x, Func1To1 expF=&std::exp)

template<class ExprT >
auto	utl::Exp (const ExprT &expr) -> decltype(utl::F< utl::Functor::Exp< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::Exp2 (const ExprT &expr) -> decltype(utl::F< utl::Functor::Exp2< typename ExprT::ValueType > >(expr))

double	utl::ExpNegtiveLUT (const double dist, const double distMax=30.0, const int precision=1000)

unsigned long	utl::Factorial (const int n)

template<typename T >
T	utl::Factorial (const T v1, const int times)

template<class ExprT >
auto	utl::Floor (const ExprT &expr) -> decltype(utl::F< utl::Functor::Floor< typename ExprT::ValueType > >(expr))

double	utl::Gamma (const double x)

double	utl::GammaHalfInteger (const double x)

double	utl::GammaLower (const double s, const double x)

template<class T >
int	utl::geev (int matrix_layout, char jobvl, char jobvr, int n, T a, int lda, T wr, T wi, T vl, int ldvl, T *vr, int ldvr)

int	utl::geev (int matrix_layout, char jobvl, char jobvr, int n, std::complex< double > a, int lda, std::complex< double > w, std::complex< double > vl, int ldvl, std::complex< double > vr, int ldvr)

template<>
int	utl::geev< double > (int matrix_layout, char jobvl, char jobvr, int n, double a, int lda, double wr, double wi, double vl, int ldvl, double *vr, int ldvr)

template<>
int	utl::geev< float > (int matrix_layout, char jobvl, char jobvr, int n, float a, int lda, float wr, float wi, float vl, int ldvl, float *vr, int ldvr)

template<>
int	utl::geev< std::complex< double > > (int matrix_layout, char jobvl, char jobvr, int n, std::complex< double > a, int lda, std::complex< double > wr, std::complex< double > wi, std::complex< double > vl, int ldvl, std::complex< double > *vr, int ldvr)

template<>
int	utl::geev< std::complex< float > > (int matrix_layout, char jobvl, char jobvr, int n, std::complex< float > a, int lda, std::complex< float > wr, std::complex< float > wi, std::complex< float > vl, int ldvl, std::complex< float > *vr, int ldvr)

template<class T >
void	utl::geev_VnlMatrix (const vnl_matrix< T > &mat, vnl_vector< T > &valReal, vnl_vector< T > &valImg, vnl_matrix< T > &vecRealR, vnl_matrix< T > &vecImgR, vnl_matrix< T > &vecRealL, vnl_matrix< T > &vecImgL)

template<class T >
void	utl::geev_VnlMatrix (const vnl_matrix< T > &mat, vnl_vector< T > &valReal, vnl_vector< T > &valImg)

template<class T >
void	utl::geev_VnlMatrix (const vnl_matrix< T > &mat, vnl_vector< T > &valReal, vnl_vector< T > &valImg, vnl_matrix< T > &vecRealR, vnl_matrix< T > &vecImgR)

template<class T >
bool	utl::gemm_VnlMatrixTimesMatrix (const bool bATrans, const bool bBTrans, const T alpha, const vnl_matrix< T > &A, const vnl_matrix< T > &B, const T beta, vnl_matrix< T > &C)

template<class T >
bool	utl::gemm_VnlVectorTimesMatrix (const bool bATrans, const T alpha, const vnl_vector< T > &X, const vnl_matrix< T > &A, const T beta, vnl_vector< T > &Y)

template<class T >
bool	utl::gemv_VnlMatrixTimesVector (const bool bATrans, const T alpha, const vnl_matrix< T > &A, const vnl_vector< T > &X, const T beta, vnl_vector< T > &Y)

template<class T >
int	utl::gesdd (int matrix_order, char JOBZ, int M, int N, T A, int LDA, T S, T U, int LDU, T VT, int LDVT)

int	utl::gesdd (int matrix_order, char JOBZ, int M, int N, std::complex< double > A, int LDA, double S, std::complex< double > U, int LDU, std::complex< double > VT, int LDVT)

int	utl::gesdd (int matrix_order, char JOBZ, int M, int N, std::complex< float > A, int LDA, float S, std::complex< float > U, int LDU, std::complex< float > VT, int LDVT)

template<>
int	utl::gesdd< double > (int matrix_order, char JOBZ, int M, int N, double A, int LDA, double S, double U, int LDU, double VT, int LDVT)

template<>
int	utl::gesdd< float > (int matrix_order, char JOBZ, int M, int N, float A, int LDA, float S, float U, int LDU, float VT, int LDVT)

template<class T >
void	utl::gesdd_VnlMatrix (const vnl_matrix< T > &mat, vnl_matrix< T > &U, vnl_vector< T > &s, vnl_matrix< T > &V, char format='S')

template<class T >
int	utl::gesvd (int matrix_order, char JOBU, char JOBVT, int M, int N, T A, int LDA, T S, T U, int LDU, T VT, int LDVT, T *superb)

template<>
int	utl::gesvd< double > (int matrix_order, char JOBU, char JOBVT, int M, int N, double A, int LDA, double S, double U, int LDU, double VT, int LDVT, double *superb)

template<>
int	utl::gesvd< float > (int matrix_order, char JOBU, char JOBVT, int M, int N, float A, int LDA, float S, float U, int LDU, float VT, int LDVT, float *superb)

template<class T >
void	utl::gesvd_VnlMatrix (const vnl_matrix< T > &mat, vnl_matrix< T > &U, vnl_vector< T > &s, vnl_matrix< T > &V, char format='S')

std::vector< double >	utl::GetCoefLaguerre (const int n, const double a=0.5)

std::vector< double >	utl::GetCoefLaguerreProduct (const int n1, const double a1, const int n2, const double a2)

template<class T >
void	utl::GetColumn (const vnl_matrix< T > &mat, const int index, vnl_vector< T > &v1)

template<class T >
void	utl::GetEqualityConstraintProjection (const vnl_matrix< T > &Aeq, const vnl_vector< T > &beq, const vnl_matrix< T > &QInverse, vnl_matrix< T > &projMatrix, vnl_vector< T > &projVector)

double	utl::GetExpLegendreCoef (const double a, const int l, Func1To1 expF=&std::exp)

double	utl::GetExpLegendreCoefDerivative (const double a, const int l, Func1To1 expF=&std::exp)

double	utl::GetExpProductLegendreCoef (const double a, const double b, const int l)

template<class T >
int	utl::getrf (int matrix_layout, int m, int n, T a, int lda, int ipiv)

template<>
int	utl::getrf< double > (int matrix_layout, int m, int n, double a, int lda, int ipiv)

template<>
int	utl::getrf< float > (int matrix_layout, int m, int n, float a, int lda, int ipiv)

template<>
int	utl::getrf< std::complex< double > > (int matrix_layout, int m, int n, std::complex< double > a, int lda, int ipiv)

template<>
int	utl::getrf< std::complex< float > > (int matrix_layout, int m, int n, std::complex< float > a, int lda, int ipiv)

template<class T >
int	utl::getri (int matrix_layout, int n, T a, int lda, const int ipiv)

template<>
int	utl::getri< double > (int matrix_layout, int n, double a, int lda, const int ipiv)

template<>
int	utl::getri< float > (int matrix_layout, int n, float a, int lda, const int ipiv)

template<>
int	utl::getri< std::complex< double > > (int matrix_layout, int n, std::complex< double > a, int lda, const int ipiv)

template<>
int	utl::getri< std::complex< float > > (int matrix_layout, int n, std::complex< float > a, int lda, const int ipiv)

template<class T >
void	utl::GetRow (const vnl_matrix< T > &mat, const int index, vnl_vector< T > &v1)

template<class T >
utl_shared_ptr< utl::NDArray< T, 1 > >	utl::GetSymmetricTensorSHCoef (const T b, const T e1, const T e2, const int lMax, const T theta=0, const T phi=0)

template<class T >
std::vector< std::vector< T > >	utl::GetSymmetricTensorSHCoefDerivative (const T b, const T e1, const T e2, const int lMax, const T theta=0, const T phi=0)

double	utl::Hyperg1F1 (double a, double b, double x)

template<class T >
T	utl::InnerProduct (const vnl_vector< T > &v1, const vnl_vector< T > &v2)

template<class TVector1 , class TVector2 >
double	utl::InnerProduct (const TVector1 &v1, const TVector2 &v2, const int N1)

template<class TMatrixType >
void	utl::InverseSmallMatrix (const TMatrixType &mat, TMatrixType &result, const int row)

template<class T >
void	utl::InverseSymmericVnlMatrix (const vnl_matrix< T > &mat, vnl_matrix< T > &result, const T eps=1e-8)

template<class T >
T	utl::Lagurre (const int n, const double a, const T x)

template<class T >
T	utl::lange (int matrix_order, char norm, int m, int n, const T *A, int LDA)

double	utl::lange (int matrix_order, char norm, int m, int n, const std::complex< double > *A, int LDA)

float	utl::lange (int matrix_order, char norm, int m, int n, const std::complex< float > *A, int LDA)

template<>
double	utl::lange< double > (int matrix_order, char norm, int m, int n, const double *A, int LDA)

template<>
float	utl::lange< float > (int matrix_order, char norm, int m, int n, const float *A, int LDA)

float	LAPACKE_clange (int matrix_order, char norm, lapack_int m, lapack_int n, const std::complex< float > *a, lapack_int lda)

double	LAPACKE_dlange (int matrix_order, char norm, lapack_int m, lapack_int n, const double *a, lapack_int lda)

float	LAPACKE_slange (int matrix_order, char norm, lapack_int m, lapack_int n, const float *a, lapack_int lda)

double	LAPACKE_zlange (int matrix_order, char norm, lapack_int m, lapack_int n, const std::complex< double > *a, lapack_int lda)

double	utl::LegendrePolynomialAt0 (const int order)

template<class ExprT >
auto	utl::Log (const ExprT &expr) -> decltype(utl::F< utl::Functor::Log< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::Log10 (const ExprT &expr) -> decltype(utl::F< utl::Functor::Log10< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::Log2 (const ExprT &expr) -> decltype(utl::F< utl::Functor::Log2< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::LRound (const ExprT &expr) -> decltype(utl::F< utl::Functor::LRound< typename ExprT::ValueType > >(expr))

template<class T >
void	utl::MatrixCopy (const vnl_matrix< T > &mat, vnl_matrix< T > &matOut, const T alpha, const char trans='N')

template<class TLeft , class TRight >
auto	utl::Max (const TLeft &lhs, const TRight &rhs) -> decltype(utl::F< utl::Functor::Max< Expr2ValueType< TLeft, TRight >> >(lhs, rhs))

template<class TLeft >
auto	utl::Max (const TLeft &lhs, const ScalarExpr &rhs) -> decltype(utl::F< utl::Functor::Max< Expr2ValueType< TLeft, ScalarExpr >> >(lhs, rhs))

template<class TRight >
auto	utl::Max (const ScalarExpr &lhs, const TRight &rhs) -> decltype(utl::F< utl::Functor::Max< Expr2ValueType< ScalarExpr, TRight >> >(lhs, rhs))

template<class TRight >
auto	utl::Min (const ScalarExpr &lhs, const TRight &rhs) -> decltype(utl::F< utl::Functor::Min< Expr2ValueType< ScalarExpr, TRight >> >(lhs, rhs))

template<class TLeft , class TRight >
auto	utl::Min (const TLeft &lhs, const TRight &rhs) -> decltype(utl::F< utl::Functor::Min< Expr2ValueType< TLeft, TRight >> >(lhs, rhs))

template<class TLeft >
auto	utl::Min (const TLeft &lhs, const ScalarExpr &rhs) -> decltype(utl::F< utl::Functor::Min< Expr2ValueType< TLeft, ScalarExpr >> >(lhs, rhs))

template<class T >
void	utl::mkl_imatcopy (const char ordering, const char trans, const int rows, const int cols, const T alpha, T *A, const int lda, const int ldb)

template<>
void	utl::mkl_imatcopy< double > (const char ordering, const char trans, const int rows, const int cols, const double alpha, double *A, const int lda, const int ldb)

template<>
void	utl::mkl_imatcopy< float > (const char ordering, const char trans, const int rows, const int cols, const float alpha, float *A, const int lda, const int ldb)

template<>
void	utl::mkl_imatcopy< std::complex< double > > (const char ordering, const char trans, const int rows, const int cols, const std::complex< double > alpha, std::complex< double > *A, const int lda, const int ldb)

template<>
void	utl::mkl_imatcopy< std::complex< float > > (const char ordering, const char trans, const int rows, const int cols, const std::complex< float > alpha, std::complex< float > *A, const int lda, const int ldb)

template<class T >
void	utl::mkl_omatcopy (const char ordering, const char trans, const int rows, const int cols, const T alpha, const T A, const int lda, T B, const int ldb)

template<>
void	utl::mkl_omatcopy< double > (const char ordering, const char trans, const int rows, const int cols, const double alpha, const double A, const int lda, double B, const int ldb)

template<>
void	utl::mkl_omatcopy< float > (const char ordering, const char trans, const int rows, const int cols, const float alpha, const float A, const int lda, float B, const int ldb)

template<>
void	utl::mkl_omatcopy< std::complex< double > > (const char ordering, const char trans, const int rows, const int cols, const std::complex< double > alpha, const std::complex< double > A, const int lda, std::complex< double > B, const int ldb)

template<>
void	utl::mkl_omatcopy< std::complex< float > > (const char ordering, const char trans, const int rows, const int cols, const std::complex< float > alpha, const std::complex< float > A, const int lda, std::complex< float > B, const int ldb)

template<class ExprT >
auto	utl::Neg (const ExprT &expr) -> decltype(utl::F< utl::Functor::Neg< typename ExprT::ValueType > >(expr))

template<class T >
void	utl::OuterProduct (const vnl_vector< T > &v1, const vnl_vector< T > &v2, vnl_matrix< T > &mat, const double alpha=1.0)

template<class T >
void	utl::OuterProduct (const vnl_vector< T > &v1, vnl_matrix< T > &mat, const double alpha=1.0)

template<class TVector1 , class TVector2 , class TMatrix >
void	utl::OuterProduct (const TVector1 &v1, const int N1, const TVector2 &v2, const int N2, TMatrix &mat)

template<class TVector1 , class TMatrix >
void	utl::OuterProduct (const TVector1 &v1, const int N1, TMatrix &mat)

template<class T >
void	utl::PInverseSymmericVnlMatrix (const vnl_matrix< T > &mat, vnl_matrix< T > &result, const T eps=1e-8)

template<class T >
void	utl::PInverseVnlMatrix (const vnl_matrix< T > &mat, vnl_matrix< T > &result, const T eps=1e-8)

std::vector< std::complex< double > >	utl::PolynomialRoot (const std::vector< double > &coef)

template<class TLeft >
auto	utl::Pow (const TLeft &lhs, const ScalarExpr &rhs) -> decltype(utl::F< utl::Functor::Pow< Expr2ValueType< TLeft, ScalarExpr >> >(lhs, rhs))

template<class TLeft , class TRight >
auto	utl::Pow (const TLeft &lhs, const TRight &rhs) -> decltype(utl::F< utl::Functor::Pow< Expr2ValueType< TLeft, TRight >> >(lhs, rhs))

template<class TRight >
auto	utl::Pow (const ScalarExpr &lhs, const TRight &rhs) -> decltype(utl::F< utl::Functor::Pow< Expr2ValueType< ScalarExpr, TRight >> >(lhs, rhs))

double	utl::PowHalfInteger (const double a, const double b)

double	utl::PowInteger (const double a, const int b)

template<class TMatrix1 , class TMatrix2 , class TMatrix3 >
void	utl::ProductMM (const TMatrix1 &mat1, int rows, int cols, const TMatrix2 &mat2, int cols2, TMatrix3 &mat3)

template<class TMatrix , class TVector1 , class TVector2 >
void	utl::ProductMv (const TMatrix &mat, int rows, int cols, const TVector1 &v1, TVector2 &v2)

template<class TVector1 , class TMatrix , class TVector2 >
void	utl::ProductvM (const TVector1 &v1, int rows, const TMatrix &mat, int cols, TVector2 &v2)

template<class T >
void	utl::ProductVnlMM (const vnl_matrix< T > &A, const vnl_matrix< T > &B, vnl_matrix< T > &C, const double alpha=1.0, const double beta=0.0)

template<class T >
void	utl::ProductVnlMM (const vnl_matrix< T > &A1, const vnl_matrix< T > &A2, const vnl_matrix< T > &A3, vnl_matrix< T > &C)

template<class T >
void	utl::ProductVnlMM (const vnl_matrix< T > &A1, const vnl_matrix< T > &A2, const vnl_matrix< T > &A3, const vnl_matrix< T > &A4, const vnl_matrix< T > &A5, vnl_matrix< T > &C)

template<class T >
void	utl::ProductVnlMM (const vnl_matrix< T > &A1, const vnl_matrix< T > &A2, const vnl_matrix< T > &A3, const vnl_matrix< T > &A4, vnl_matrix< T > &C)

template<class T >
void	utl::ProductVnlMMt (const vnl_matrix< T > &A, const vnl_matrix< T > &B, vnl_matrix< T > &C, const double alpha=1.0, const double beta=0.0)

template<class T >
void	utl::ProductVnlMtM (const vnl_matrix< T > &A, const vnl_matrix< T > &B, vnl_matrix< T > &C, const double alpha=1.0, const double beta=0.0)

template<class T >
void	utl::ProductVnlMtMt (const vnl_matrix< T > &A, const vnl_matrix< T > &B, vnl_matrix< T > &C, const double alpha=1.0, const double beta=0.0)

template<class T >
void	utl::ProductVnlMtv (const vnl_matrix< T > &A, const vnl_vector< T > &b, vnl_vector< T > &c, const double alpha=1.0, const double beta=0.0)

template<class T >
void	utl::ProductVnlMv (const vnl_matrix< T > &A, const vnl_vector< T > &b, vnl_vector< T > &c, const double alpha=1.0, const double beta=0.0)

template<class T >
void	utl::ProductVnlvM (const vnl_vector< T > &b, const vnl_matrix< T > &A, vnl_vector< T > &c, const double alpha=1.0, const double beta=0.0)

template<class T >
void	utl::ProductVnlvMt (const vnl_vector< T > &b, const vnl_matrix< T > &A, vnl_vector< T > &c, const double alpha=1.0, const double beta=0.0)

template<class T >
void	utl::ProductVnlXtX (const vnl_matrix< T > &A, vnl_matrix< T > &C, const double alpha=1.0, const double beta=0.0)

template<class T >
void	utl::ProductVnlXXt (const vnl_matrix< T > &A, vnl_matrix< T > &C, const double alpha=1.0, const double beta=0.0)

template<class VectorType , class MatrixType >
void	utl::RotationMatrixFromUnitNormVectors (const VectorType &from, const VectorType &to, MatrixType &mtx)

template<class VectorType , class MatrixType >
void	utl::RotationMatrixFromVectors (const VectorType &from, const VectorType &to, MatrixType &mat)

template<class ExprT >
auto	utl::Round (const ExprT &expr) -> decltype(utl::F< utl::Functor::Round< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::Sign (const ExprT &expr) -> decltype(utl::F< utl::Functor::Sign< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::Sin (const ExprT &expr) -> decltype(utl::F< utl::Functor::Sin< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::Sqrt (const ExprT &expr) -> decltype(utl::F< utl::Functor::Sqrt< typename ExprT::ValueType > >(expr))

template<class ExprT >
auto	utl::Square (const ExprT &expr) -> decltype(utl::F< utl::Functor::Square< typename ExprT::ValueType > >(expr))

template<class TVector1 >
double	utl::SquaredTwoNorm (const TVector1 &v1, const int N1)

template<class T >
void	utl::SVDVnlMatrix (const vnl_matrix< T > &mat, vnl_matrix< T > &U, vnl_vector< T > &s, vnl_matrix< T > &V, char format='S')

template<class T >
int	utl::syev (int matrix_order, char JOBZ, char UPLO, int N, T A, int LDA, T W)

template<>
int	utl::syev< double > (int matrix_order, char JOBZ, char UPLO, int N, double A, int LDA, double W)

template<>
int	utl::syev< float > (int matrix_order, char JOBZ, char UPLO, int N, float A, int LDA, float W)

template<class T >
void	utl::syev_VnlMatrix (const vnl_matrix< T > &mat, vnl_vector< T > &eigenValues, vnl_matrix< T > &eigenVectors)

template<class T >
int	utl::syevd (int matrix_order, char JOBZ, char UPLO, int N, T A, int LDA, T W)

template<>
int	utl::syevd< double > (int matrix_order, char JOBZ, char UPLO, int N, double A, int LDA, double W)

template<>
int	utl::syevd< float > (int matrix_order, char JOBZ, char UPLO, int N, float A, int LDA, float W)

template<>
int	utl::syevd< std::complex< double > > (int matrix_order, char JOBZ, char UPLO, int N, std::complex< double > A, int LDA, std::complex< double > W)

template<>
int	utl::syevd< std::complex< float > > (int matrix_order, char JOBZ, char UPLO, int N, std::complex< float > A, int LDA, std::complex< float > W)

template<class T >
void	utl::syevd_VnlMatrix (const vnl_matrix< T > &mat, vnl_vector< T > &eigenValues, vnl_matrix< T > &eigenVectors)

template<class T >
void	utl::syrk_VnlMatrix (const bool trans, const T alpha, const vnl_matrix< T > &A, const T beta, vnl_matrix< T > &C)

template<class T >
int	utl::sytrf (int matrix_order, char UPLO, int N, T A, int LDA, int IPIV)

template<>
int	utl::sytrf< double > (int matrix_order, char UPLO, int N, double A, int LDA, int IPIV)

template<>
int	utl::sytrf< float > (int matrix_order, char UPLO, int N, float A, int LDA, int IPIV)

template<>
int	utl::sytrf< std::complex< double > > (int matrix_order, char UPLO, int N, std::complex< double > A, int LDA, int IPIV)

template<>
int	utl::sytrf< std::complex< float > > (int matrix_order, char UPLO, int N, std::complex< float > A, int LDA, int IPIV)

template<class T >
int	utl::sytri (int matrix_order, char UPLO, int N, T A, int LDA, const int IPIV)

template<>
int	utl::sytri< double > (int matrix_order, char UPLO, int N, double A, int LDA, const int IPIV)

template<>
int	utl::sytri< float > (int matrix_order, char UPLO, int N, float A, int LDA, const int IPIV)

template<>
int	utl::sytri< std::complex< double > > (int matrix_order, char UPLO, int N, std::complex< double > A, int LDA, const int IPIV)

template<>
int	utl::sytri< std::complex< float > > (int matrix_order, char UPLO, int N, std::complex< float > A, int LDA, const int IPIV)

template<class ExprT >
auto	utl::Tan (const ExprT &expr) -> decltype(utl::F< utl::Functor::Tan< typename ExprT::ValueType > >(expr))

double	utl::w_im (double x)

static double	utl::w_im_y100 (double y100, double x)

Variables
static const double	utl::BesselJPrimeZerosOrder1 [60]

static const double	utl::BesselJPrimeZerosTable []

static constexpr double	utl::E = 2.71828182845904523536028747135

static const unsigned long	utl::FactorialTable [21]

static const double	utl::GammaHalfIntegerTable [30]

static constexpr double	utl::LOG10E = 0.43429448190325182765112891892

static constexpr double	utl::LOG2E = 1.44269504088896340735992468100

static constexpr double	utl::PI = 3.14159265358979323846264338328

static constexpr double	utl::PI_2 = 1.57079632679489661923132169164

static constexpr double	utl::PI_4 = 0.78539816339744830961566084582

static constexpr double	utl::SQRT1_2 = 0.70710678118654752440084436210

static constexpr double	utl::SQRT2 = 1.41421356237309504880168872421

static constexpr double	utl::SQRT3 = 1.73205080756887729352744634151

static constexpr double	utl::SQRTPI = 1.77245385090551602729816748334

Detailed Description

math related helper functions.

Macro Definition Documentation

#define __utl_geev_Matrix	(	T,
		FuncName,
		RowMajorMatrixName,
		GetRowsFuncName,
		GetColsFuncName,
		MatrixGetDataFuncName,
		VectorName,
		VectorGetDataFuncName,
		ReSizeFuncName
	)

geev_VnlMatrix Calculate non-symmetric eigen-decomposition. Define 3 functions. 1) calculate only eigenvalues. 2) eigenvalues, right eigenvectors. 3) eigenvalues, right eigenvectors, left eigenvectors.

Parameters

mat	matrix with size NxN.
valReal	real part of right eigen-values.
valImg	imginary part of right eigen-values.
vecRealR	real part of right eigen-vectors.
vecImgR	part of right eigen-vectors.
vecRealL	real part of left eigen-vectors.
vecImgL	part of left eigen-vectors.

http://www.netlib.org/lapack/explore-html/d9/d8e/group__double_g_eeigen_ga8ec1625302675b981eb34ed024b27a47.html http://www.netlib.org/lapack/lug/node31.html

Definition at line 355 of file utlLapack.h.

#define __utl_gemm_MatrixTimesMatrix	(	T,
		FuncName,
		FuncHelperName,
		RowMajorMatrixName,
		GetRowsFuncName,
		GetColsFuncName,
		GetDataFuncName,
		ReSizeFuncName
	)

macro to define gemm for row-major matrix product

http://www.netlib.org/lapack/explore-html/d7/d2b/dgemm_8f.html https://developer.apple.com/library/mac/documentation/Accelerate/Reference/BLAS_Ref/Reference/reference.html

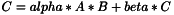
$ C = alpha * A * B + beta * C $

Note: : C should be pre-allocated

Definition at line 433 of file utlBlas.h.

#define __utl_gemv_MatrixTimesVector	(	T,
		FuncName,
		FuncHelperName,
		RowMajorMatrixName,
		GetRowsFuncName,
		GetColsFuncName,
		MatrixGetDataFuncName,
		VectorName,
		GetSizeFuncName,
		VectorGetDataFuncName,
		ReSizeFuncName
	)

macro to define gemm for row-major matrix and vector product

http://www.netlib.org/lapack/explore-html/d7/d2b/dgemm_8f.html https://developer.apple.com/library/mac/documentation/Accelerate/Reference/BLAS_Ref/Reference/reference.html

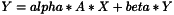
$ Y = alpha * A * X + beta * Y $

Note: : Y should be pre-allocated

Definition at line 551 of file utlBlas.h.

#define __utl_getri_Matrix	(	T,
		FuncName,
		RowMajorMatrixName,
		GetRowsFuncName,
		GetColsFuncName,
		MatrixGetDataFuncName,
		ReSizeFuncName
	)

Value:

template <class T> inline void                                                                                                                                                      \
FuncName(const RowMajorMatrixName& mat, RowMajorMatrixName& result)                                                                                                                 \
{                                                                                                                                                                                   \
  int N = mat.GetRowsFuncName(),INFO=0;                                                                                                                                             \
  int ipiv[N];                                                                                                                                                                      \
  result = mat;                                                                                                                                                                     \
  INFO = getrf<T>(LAPACK_ROW_MAJOR, N,N,result.MatrixGetDataFuncName(),N,ipiv);                                                                                                     \
  INFO = getri<T>(LAPACK_ROW_MAJOR, N,result.MatrixGetDataFuncName(),N,ipiv);                                                                                                       \
}

Definition at line 321 of file utlLapack.h.

#define __utl_gevm_MatrixTimesVector	(	T,
		FuncName,
		FuncHelperName,
		RowMajorMatrixName,
		GetRowsFuncName,
		GetColsFuncName,
		MatrixGetDataFuncName,
		VectorName,
		GetSizeFuncName,
		VectorGetDataFuncName,
		ReSizeFuncName
	)

$ Y = alpha X^T * A + beta * Y $

Note: : Y should be pre-allocated

Definition at line 593 of file utlBlas.h.

#define __utl_syrk_Matrix	(	T,
		FuncName,
		FuncHelperName,
		RowMajorMatrixName,
		GetRowsFuncName,
		GetColsFuncName,
		GetDataFuncName,
		ReSizeFuncName
	)

macro for syrk and row-major matrix

Parameters

trans	If false, then C := alpha* AA' + beta C; If true, then C := alpha* A'A + beta C
alpha
A	MxN matrix
beta
C	MxM or NxN symmetric matrix

Definition at line 646 of file utlBlas.h.

#define lapack_complex_double std::complex<double>

Definition at line 39 of file utlLapack.h.

#define lapack_complex_float std::complex<float>

Definition at line 40 of file utlLapack.h.

Typedef Documentation

typedef double(* utl::Func1To1) (double)

Definition at line 32 of file utlMath.h.

Function Documentation

template<class ExprT >

auto utl::Abs ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Abs <typename ExprT::ValueType> >(expr))

Definition at line 356 of file utlFunctors.h.

Referenced by itk::SamplingSchemeQSpace1OptEstimationFilter< TSamplingType >::GenerateData().

Here is the caller graph for this function:

template<class ExprT >

auto utl::Acos ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Acos <typename ExprT::ValueType> >(expr))

Definition at line 375 of file utlFunctors.h.

template<class ExprT >

auto utl::Asin ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Asin <typename ExprT::ValueType> >(expr))

Definition at line 374 of file utlFunctors.h.

template<class ExprT >

auto utl::Atan ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Atan <typename ExprT::ValueType> >(expr))

Definition at line 376 of file utlFunctors.h.

template<class TLeft >

auto utl::Atan2	(	const TLeft &	lhs,
		const ScalarExpr &	rhs
	)		-> decltype(utl::F<utl::Functor:: Atan2 <Expr2ValueType<TLeft,ScalarExpr>> >(lhs, rhs))

Definition at line 386 of file utlFunctors.h.

template<class TRight >

auto utl::Atan2	(	const ScalarExpr &	lhs,
		const TRight &	rhs
	)		-> decltype(utl::F<utl::Functor:: Atan2 <Expr2ValueType<ScalarExpr,TRight>> >(lhs, rhs))

Definition at line 386 of file utlFunctors.h.

template<class TLeft , class TRight >

auto utl::Atan2	(	const TLeft &	lhs,
		const TRight &	rhs
	)		-> decltype(utl::F<utl::Functor:: Atan2 <Expr2ValueType<TLeft,TRight>> >(lhs, rhs))

Definition at line 386 of file utlFunctors.h.

double utl::BesselJa	(	const double	a,
		const double	x
	)

inline

bessel_Ja : Regular Cylindrical Bessel Function 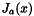$ J_a(x) $

Parameters

a	: should be an integer or half of an integer
x	: float number

Note: gsl_sf_bessel_Jn(a,x) in gsl only works when a is integer

Returns

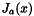
Definition at line 84 of file itkSpecialFunctionGenerator.hxx.

References spams::abs(), utl::BesselJInteger(), M_PI, and utlException.

Here is the call graph for this function:

double utl::BesselJInteger	(	const int	n,
		const double	x
	)

inline

Definition at line 106 of file itkSpecialFunctionGenerator.hxx.

Referenced by utl::BesselJa(), and utl::BesselJIntegerPrime().

Here is the caller graph for this function:

double utl::BesselJIntegerPrime	(	const int	n,
		const double	x
	)

inline

Definition at line 119 of file itkSpecialFunctionGenerator.hxx.

References utl::BesselJInteger().

Here is the call graph for this function:

template<typename T >

T utl::Binomial	(	const T	v1,
		const int	times
	)

inline

generalized binomial coefficients

Note: if times==0, return 1 whatever v1 is.

Definition at line 219 of file utlMath.h.

References utl::Factorial(), and utlException.

Here is the call graph for this function:

template<class T >

utl_shared_ptr< utl::NDArray< T, 1 > > utl::ComputeDWISHCoefficientsForGPDCylinder	(	const T	radius,
		const T	diffusivity,
		const T	deltaBig,
		const T	deltaSmall,
		const T	qq,
		const int	lMax,
		const T	theta = `0`,
		const T	phi = `0`
	)

Calculate SH coefficients of DWI samples in Cylinder GPD model. (theta,phi) is the direction of the cylinder. Reference: Compartment models of the diffusion MR signal in brain white matter: A taxonomy and comparison, NeuroImage 2012.

Definition at line 256 of file itkSpecialFunctionGenerator.hxx.

References utl::BesselJPrimeZerosOrder1, utl::GetExpProductLegendreCoef(), utl::GetIndexSHj(), itk::lutExpValue(), M_PI, utl::RankToDimSH(), itk::SphericalHarmonicsGenerator< PreciseType >::RealSH(), and utl::SQRTPI.

Here is the call graph for this function:

template<class T >

double utl::ComputeOrientationalOrderFromSHCoefficients	(	const utl::NDArray< T, 1 > &	shCoef,
		const utl::NDArray< T, 1 > &	axis
	)

Calculate Orientational Order with a given axis from sh coefficients. It is 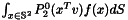$\int_{x \in \mathbb{S}^2} P_2^0(x^Tv) f(x) d S$ , where 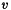$v$ is the axis.

Refernce: https://en.wikipedia.org/wiki/Liquid_crystal#Order_parameter

Definition at line 316 of file itkSpecialFunctionGenerator.hxx.

References utl::GetIndexSHj(), utl::NDArrayBase< T, Dim >::GetSquaredTwoNorm(), M_PI, utl::RankToDimSH(), utl::RotationMatrixFromVectors(), utl::NDArrayBase< T, Dim >::Size(), utlException, and utlSAException.

Here is the call graph for this function:

double utl::ComputeOrientationalOrderFromSymmetricTensor	(	const double	e1,
		const double	e2,
		const double	phi = `0`
	)

inline

Calculate orientation order for a axisymmetric tensor (e1,e2,e2).

Parameters

phi	it is the angle between principal direction of tensor (v1) and the orientaiton axis (n).

Definition at line 348 of file itkSpecialFunctionGenerator.hxx.

References utl::IsSame().

Here is the call graph for this function:

template<class ExprT >

auto utl::Conj ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Conj <typename ExprT::ValueType> >(expr))

Definition at line 380 of file utlFunctors.h.

Referenced by utl::NDArray< T, 2 >::GetConjugateTranspose().

Here is the caller graph for this function:

template<class ExprT >

auto utl::Cos ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Cos <typename ExprT::ValueType> >(expr))

Definition at line 372 of file utlFunctors.h.

template<class TVector1 , class TVector2 , class TVector3 >

double utl::CrossProduct	(	const TVector1 &	v1,
		const TVector2 &	v2,
		TVector3 &	v3
	)

inline

Cross product of two 3d vectors. v3 needs to be pre-allocated.

Definition at line 1350 of file utlMath.h.

Referenced by utl::NDArray< T, 1 >::GetRotateAxis().

Here is the caller graph for this function:

template<class ExprT >

auto utl::Cube ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Cube <typename ExprT::ValueType> >(expr))

Definition at line 369 of file utlFunctors.h.

double utl::DawsonF ( double x )

inline

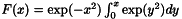
$F(x) = \exp(-x^2) \int_0^x \exp(y^2) dy$

Definition at line 712 of file utlMath.h.

References utl::SQRTPI, and utl::w_im_y100().

Here is the call graph for this function:

template<class TMatrixType >

auto utl::DeterminantSmallMatrix	(	const TMatrixType &	mat,
		const int	row
	)		-> utl::remove_reference_t<decltype(mat(0,0))>

inline

Calculate determinant of a small matrix with (i,j) defined.

Parameters

row	shoud be in [1,4].

Definition at line 1163 of file utlMath.h.

template<class TVector1 , class TVector2 >

double utl::DotProduct	(	const TVector1 &	v1,
		const TVector2 &	v2,
		const int	N1
	)

inline

Definition at line 1332 of file utlMath.h.

Referenced by utl::NDArray< T, 1 >::GetRotateAxis().

Here is the caller graph for this function:

template<class T >

void utl::EigenDecompositionSymmetricVnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_vector< T > &	eigenValues,
		vnl_matrix< T > &	eigenVectors
	)

inline

EigenDecompositionSymmetricVnlMatrix eigen-decomposition for symmetric matrix.

Parameters

mat	a symmetric matrix (only upper triangular matrix is used)
eigenValues	Eigen-values are in increasing order.
eigenVectors	Eigen-vectors. each row is an eigen-vector

Definition at line 249 of file utlVNLLapack.h.

Referenced by utl::PInverseSymmericVnlMatrix().

Here is the caller graph for this function:

template<class VectorType >

double utl::Entropy	(	const VectorType &	pdfVec,
		const int	N
	)

inline

Calculate entropy from a discrete pdf with N elements. Assume it is already normalized so that the sum is 1.

Definition at line 702 of file utlMath.h.

Referenced by itk::SamplingScheme3D< TPixelType >::CalculateSphericalCodeEntropy(), itk::SamplingScheme3D< TPixelType >::CalculateSphericalCodeEntropyInShell(), and itk::SamplingScheme3D< TPixelType >::CalculateVoronoiEntropy().

Here is the caller graph for this function:

double utl::Erf ( double x )

inline

Definition at line 694 of file utlMath.h.

double utl::Erfi	(	double	x,
		Func1To1	expF = `&std::exp`
	)

inline

erfi(x) = -i erf(ix). See http://ab-initio.mit.edu/wiki/index.php/Faddeeva_Package

Definition at line 687 of file utlMath.h.

References utl::w_im().

Here is the call graph for this function:

template<class ExprT >

auto utl::Exp ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Exp <typename ExprT::ValueType> >(expr))

Definition at line 357 of file utlFunctors.h.

template<class ExprT >

auto utl::Exp2 ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Exp2 <typename ExprT::ValueType> >(expr))

Definition at line 358 of file utlFunctors.h.

double utl::ExpNegtiveLUT	(	const double	dist,
		const double	distMax = `30.0`,
		const int	precision = `1000`
	)

inline

calculate exp(-dist) using LUT

Definition at line 132 of file utlMath.h.

unsigned long utl::Factorial ( const int n )

inline

factorial of non-negative value n using a static table.

Definition at line 190 of file utlMath.h.

References utlException.

Referenced by itk::ScalarMapFromSPFImageFilter< TInputImage, TOutputImage >::BeforeThreadedGenerateData(), utl::Binomial(), itk::SphericalPolarFourierRadialGenerator< PreciseType >::Evaluate(), itk::SphericalPolarFourierRadialGenerator< PreciseType >::GetNormalizeFacotr(), and itk::ScalarMapFromSPFImageFilter< TInputImage, TOutputImage >::ThreadedGenerateData().

Here is the caller graph for this function:

template<typename T >

T utl::Factorial	(	const T	v1,
		const int	times
	)

inline

Definition at line 203 of file utlMath.h.

template<class ExprT >

auto utl::Floor ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Floor <typename ExprT::ValueType> >(expr))

Definition at line 363 of file utlFunctors.h.

double utl::Gamma ( const double x )

inline

gamma function.

Parameters

x	real value. If x is positive integer, the result is factorial(x). If x is a half of a positive integer, the result is analytical with gamma(0.5)=(). If x is other real number, it returns the result of gsl_sf_gamma().

Definition at line 65 of file itkSpecialFunctionGenerator.hxx.

References utl::GammaHalfInteger(), utl::IsInt(), and utlException.

Referenced by itk::SphericalHarmonicsGenerator< PreciseType >::ComplexDerivativeOfTheta(), utl::GammaLower(), and itk::ScalarMapFromSPFImageFilter< TInputImage, TOutputImage >::ThreadedGenerateData().

Here is the call graph for this function:

Here is the caller graph for this function:

double utl::GammaHalfInteger ( const double x )

inline

Calculate Gamma function for an input which is 0.5,1,1.5,2,2.5,... etc.

Definition at line 887 of file utlMath.h.

Referenced by itk::ScalarMapFromSPFImageFilter< TInputImage, TOutputImage >::BeforeThreadedGenerateData(), itk::SphericalPolarFourierRadialGenerator< PreciseType >::Evaluate(), utl::Gamma(), and itk::SphericalPolarFourierRadialGenerator< PreciseType >::GetNormalizeFacotr().

Here is the caller graph for this function:

double utl::GammaLower	(	const double	s,
		const double	x
	)

inline

Definition at line 76 of file itkSpecialFunctionGenerator.hxx.

References utl::Gamma().

Here is the call graph for this function:

template<class T >

int utl::geev	(	int	matrix_layout,
		char	jobvl,
		char	jobvr,
		int	n,
		T *	a,
		int	lda,
		T *	wr,
		T *	wi,
		T *	vl,
		int	ldvl,
		T *	vr,
		int	ldvr
	)

inline

int utl::geev	(	int	matrix_layout,
		char	jobvl,
		char	jobvr,
		int	n,
		std::complex< double > *	a,
		int	lda,
		std::complex< double > *	w,
		std::complex< double > *	vl,
		int	ldvl,
		std::complex< double > *	vr,
		int	ldvr
	)

inline

Definition at line 232 of file utlLapack.h.

template<>

int utl::geev< double >	(	int	matrix_layout,
		char	jobvl,
		char	jobvr,
		int	n,
		double *	a,
		int	lda,
		double *	wr,
		double *	wi,
		double *	vl,
		int	ldvl,
		double *	vr,
		int	ldvr
	)

inline

Definition at line 220 of file utlLapack.h.

template<>

int utl::geev< float >	(	int	matrix_layout,
		char	jobvl,
		char	jobvr,
		int	n,
		float *	a,
		int	lda,
		float *	wr,
		float *	wi,
		float *	vl,
		int	ldvl,
		float *	vr,
		int	ldvr
	)

inline

Definition at line 223 of file utlLapack.h.

template<>

int utl::geev< std::complex< double > >	(	int	matrix_layout,
		char	jobvl,
		char	jobvr,
		int	n,
		std::complex< double > *	a,
		int	lda,
		std::complex< double > *	wr,
		std::complex< double > *	wi,
		std::complex< double > *	vl,
		int	ldvl,
		std::complex< double > *	vr,
		int	ldvr
	)

inline

Definition at line 226 of file utlLapack.h.

References utlGlobalException.

template<>

int utl::geev< std::complex< float > >	(	int	matrix_layout,
		char	jobvl,
		char	jobvr,
		int	n,
		std::complex< float > *	a,
		int	lda,
		std::complex< float > *	wr,
		std::complex< float > *	wi,
		std::complex< float > *	vl,
		int	ldvl,
		std::complex< float > *	vr,
		int	ldvr
	)

inline

Definition at line 229 of file utlLapack.h.

References utlGlobalException.

template<class T >

void utl::geev_VnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_vector< T > &	valReal,
		vnl_vector< T > &	valImg,
		vnl_matrix< T > &	vecRealR,
		vnl_matrix< T > &	vecImgR,
		vnl_matrix< T > &	vecRealL,
		vnl_matrix< T > &	vecImgL
	)

inline

geev_VnlMatrix calculate non-symmetric eigen-decomposition.

Parameters

mat	matrix with size NxN.
valReal	real part of right eigen-values.
valImg	imginary part of right eigen-values.
vecRealR	real part of right eigen-vectors.
vecImgR	part of right eigen-vectors.
vecRealL	real part of left eigen-vectors.
vecImgL	part of left eigen-vectors.

template <class T> inline void geev_VnlMatrix ( const vnl_matrix<T>& mat, vnl_vector<T>& valReal, vnl_vector<T>& valImg);

template <class T> inline void geev_VnlMatrix ( const vnl_matrix<T>& mat, vnl_vector<T>& valReal, vnl_vector<T>& valImg, vnl_matrix<T>& vecRealR, vnl_matrix<T>& vecImgR);

template <class T> inline void geev_VnlMatrix ( const vnl_matrix<T>& mat, vnl_vector<T>& valReal, vnl_vector<T>& valImg, vnl_matrix<T>& vecRealR, vnl_matrix<T>& vecImgR, vnl_matrix<T>& vecRealL, vnl_matrix<T>& vecImgL);

http://www.netlib.org/lapack/explore-html/d9/d8e/group__double_g_eeigen_ga8ec1625302675b981eb34ed024b27a47.html http://www.netlib.org/lapack/lug/node31.html

Definition at line 59 of file utlVNLLapack.h.

template<class T >

void utl::geev_VnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_vector< T > &	valReal,
		vnl_vector< T > &	valImg
	)

inline

Definition at line 59 of file utlVNLLapack.h.

template<class T >

void utl::geev_VnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_vector< T > &	valReal,
		vnl_vector< T > &	valImg,
		vnl_matrix< T > &	vecRealR,
		vnl_matrix< T > &	vecImgR
	)

inline

Definition at line 59 of file utlVNLLapack.h.

template<class T >

bool utl::gemm_VnlMatrixTimesMatrix	(	const bool	bATrans,
		const bool	bBTrans,
		const T	alpha,
		const vnl_matrix< T > &	A,
		const vnl_matrix< T > &	B,
		const T	beta,
		vnl_matrix< T > &	C
	)

inline

http://www.netlib.org/lapack/explore-html/d7/d2b/dgemm_8f.html https://developer.apple.com/library/mac/documentation/Accelerate/Reference/BLAS_Ref/Reference/reference.html

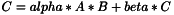
$ C = alpha * A * B + beta * C $

Note: : C should be pre-allocated

define several functions.

template <class T> inline bool gemm_VnlMatrixTimesMatrix(const bool bATrans, const bool bBTrans, const T alpha, const vnl_matrix<T>& a, const vnl_matrix<T>& b, const T beta, vnl_matrix<T>& c);

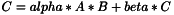
$ C = alpha * A * B + beta * C $
template <class T> inline void ProductVnlMM(const vnl_matrix<T>& A, const vnl_matrix<T>& B, vnl_matrix<T>& C, const double alpha=1.0, const double beta=0.0);

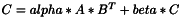
$ C = alpha * A * B^T + beta * C $
template <class T> inline void ProductVnlMMt(const vnl_matrix<T>& A, const vnl_matrix<T>& B, vnl_matrix<T>& C, const double alpha=1.0, const double beta=0.0);

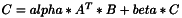
$ C = alpha * A^T * B + beta * C $
template <class T> inline void ProductVnlMtM(const vnl_matrix<T>& A, const vnl_matrix<T>& B, vnl_matrix<T>& C, const double alpha=1.0, const double beta=0.0);

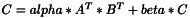
$ C = alpha * A^T * B^T + beta * C $
template <class T> inline void ProductVnlMtMt(const vnl_matrix<T>& A, const vnl_matrix<T>& B, vnl_matrix<T>& C, const double alpha=1.0, const double beta=0.0);

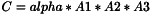
$ C = alpha * A1*A2*A3 $
template <class T> inline void ProductVnlMM(const vnl_matrix<T>& A1, const vnl_matrix<T>& A2, const vnl_matrix<T>& A3, vnl_matrix<T>& C);

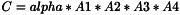
$ C = alpha * A1*A2*A3*A4 $
template <class T> inline void ProductVnlMM(const vnl_matrix<T>& A1, const vnl_matrix<T>& A2, const vnl_matrix<T>& A3, const vnl_matrix<T>& A4, vnl_matrix<T>& C);

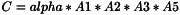
$ C = alpha * A1*A2*A3*A5 $
template <class T> inline void ProductVnlMM(const vnl_matrix<T>& A1, const vnl_matrix<T>& A2, const vnl_matrix<T>& A3, const vnl_matrix<T>& A4, const vnl_matrix<T>& A5, vnl_matrix<T>& C);

Definition at line 117 of file utlVNLBlas.h.

template<class T >

bool utl::gemm_VnlVectorTimesMatrix	(	const bool	bATrans,
		const T	alpha,
		const vnl_vector< T > &	X,
		const vnl_matrix< T > &	A,
		const T	beta,
		vnl_vector< T > &	Y
	)

inline

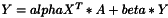
$ Y = alpha X^T * A + beta * Y $

Note: : Y should be pre-allocated

define several functions.

template <class T> inline bool gemm_VnlVectorTimesMatrix(const bool bATrans, const T alpha, const vnl_vector<T>& X, const vnl_matrix<T>& A, const T beta, vnl_vector<T>& Y)

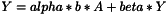
$ Y = alpha * b * A + beta * Y $
template <class T> inline void ProductVnlvM(const vnl_vector<T>& b, const vnl_matrix<T>& A, vnl_vector<T>& c, const double alpha=1.0, const double beta=0.0)

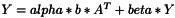
$ Y = alpha * b * A^T + beta * Y $
template <class T> inline void ProductVnlvMt(const vnl_vector<T>& b, const vnl_matrix<T>& A, vnl_vector<T>& c, const double alpha=1.0, const double beta=0.0)

Definition at line 161 of file utlVNLBlas.h.

template<class T >

bool utl::gemv_VnlMatrixTimesVector	(	const bool	bATrans,
		const T	alpha,
		const vnl_matrix< T > &	A,
		const vnl_vector< T > &	X,
		const T	beta,
		vnl_vector< T > &	Y
	)

inline

http://www.netlib.org/lapack/explore-html/d7/d2b/dgemm_8f.html https://developer.apple.com/library/mac/documentation/Accelerate/Reference/BLAS_Ref/Reference/reference.html

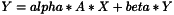
$ Y = alpha * A * X + beta * Y $

Note: : Y should be pre-allocated

define several functions.

template <class T> inline bool gemv_VnlMatrixTimesVector(const bool bATrans, const T alpha, const vnl_matrix<T>& A, const vnl_vector<T>& X, const T beta, vnl_vector<T>& Y);

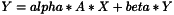
$ Y = alpha * A * X + beta * Y $
template <class T> inline void ProductVnlMv(const vnl_matrix<T>& A, const vnl_vector<T>& b, vnl_vector<T>& c, const double alpha=1.0, const double beta=0.0);

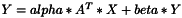
$ Y = alpha * A^T * X + beta * Y $
template <class T> inline void ProductVnlMtv(const vnl_matrix<T>& A, const vnl_vector<T>& b, vnl_vector<T>& c, const double alpha=1.0, const double beta=0.0);

Definition at line 140 of file utlVNLBlas.h.

template<class T >

int utl::gesdd	(	int	matrix_order,
		char	JOBZ,
		int	M,
		int	N,
		T *	A,
		int	LDA,
		T *	S,
		T *	U,
		int	LDU,
		T *	VT,
		int	LDVT
	)

inline

Referenced by utl::gesdd_UtlMatrix().

Here is the caller graph for this function:

int utl::gesdd	(	int	matrix_order,
		char	JOBZ,
		int	M,
		int	N,
		std::complex< double > *	A,
		int	LDA,
		double *	S,
		std::complex< double > *	U,
		int	LDU,
		std::complex< double > *	VT,
		int	LDVT
	)

inline

Definition at line 249 of file utlLapack.h.

int utl::gesdd	(	int	matrix_order,
		char	JOBZ,
		int	M,
		int	N,
		std::complex< float > *	A,
		int	LDA,
		float *	S,
		std::complex< float > *	U,
		int	LDU,
		std::complex< float > *	VT,
		int	LDVT
	)

inline

Definition at line 252 of file utlLapack.h.

template<>

int utl::gesdd< double >	(	int	matrix_order,
		char	JOBZ,
		int	M,
		int	N,
		double *	A,
		int	LDA,
		double *	S,
		double *	U,
		int	LDU,
		double *	VT,
		int	LDVT
	)

inline

Definition at line 243 of file utlLapack.h.

template<>

int utl::gesdd< float >	(	int	matrix_order,
		char	JOBZ,
		int	M,
		int	N,
		float *	A,
		int	LDA,
		float *	S,
		float *	U,
		int	LDU,
		float *	VT,
		int	LDVT
	)

inline

Definition at line 246 of file utlLapack.h.

template<class T >

void utl::gesdd_VnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_matrix< T > &	U,
		vnl_vector< T > &	s,
		vnl_matrix< T > &	V,
		char	format = `'S'`
	)

inline

dgesdd_VnlMatrix dgesdd is faster than dgesvd. http://www.netlib.org/lapack/explore-html/db/db4/dgesdd_8f.html http://www.netlib.org/lapack/lug/node71.html

Parameters

mat	matrix with size MxN.
U	left singular vectors. If format is 'A', U is MxM matrix. If format is 'S', U size is M x min(M,N)
s	singular values with size min(M,N). Sored in decreasing order.
V	right singular vectors. If format is 'A', V size is NxN. If format is 'S', V size is N x min(M,N)
format	'S' or 'A'. 'A' means full size, 'S' means reduced size.

Definition at line 194 of file utlVNLLapack.h.

References utl::MatrixCopy(), utl::min(), utlException, and utlGlobalException.

Here is the call graph for this function:

template<class T >

int utl::gesvd	(	int	matrix_order,
		char	JOBU,
		char	JOBVT,
		int	M,
		int	N,
		T *	A,
		int	LDA,
		T *	S,
		T *	U,
		int	LDU,
		T *	VT,
		int	LDVT,
		T *	superb
	)

inline

template<>

int utl::gesvd< double >	(	int	matrix_order,
		char	JOBU,
		char	JOBVT,
		int	M,
		int	N,
		double *	A,
		int	LDA,
		double *	S,
		double *	U,
		int	LDU,
		double *	VT,
		int	LDVT,
		double *	superb
	)

inline

Definition at line 236 of file utlLapack.h.

template<>

int utl::gesvd< float >	(	int	matrix_order,
		char	JOBU,
		char	JOBVT,
		int	M,
		int	N,
		float *	A,
		int	LDA,
		float *	S,
		float *	U,
		int	LDU,
		float *	VT,
		int	LDVT,
		float *	superb
	)

inline

Definition at line 239 of file utlLapack.h.

template<class T >

void utl::gesvd_VnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_matrix< T > &	U,
		vnl_vector< T > &	s,
		vnl_matrix< T > &	V,
		char	format = `'S'`
	)

inline

dgesvd_VnlMatrix

Parameters

mat	matrix with size MxN.
U	left singular vectors. If format is 'A', U is MxM matrix. If format is 'S', U size is M x min(M,N)
s	singular values with size min(M,N). Sored in decreasing order.
V	right singular vectors. If format is 'A', V size is NxN. If format is 'S', V size is N x min(M,N)
format	'S' or 'A'. 'A' means full size, 'S' means reduced size.

Definition at line 140 of file utlVNLLapack.h.

References utl::MatrixCopy(), utl::min(), utlException, and utlGlobalException.

Here is the call graph for this function:

std::vector<double> utl::GetCoefLaguerre	(	const int	n,
		const double	a = `0.5`
	)

inline

Get the coefficient vector of nth order Lagurre polynomial L_n^{alpha}(x). The default value of alpha is 0.5 for DiffusionMRI::EAP class.

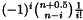Note: the ith coefficient of n order Lagurre polynomial has a closed form $(-1)^i\binom{n+0.5}{n-i}\frac{1}{i!}$ . But here we use a recursive way that is more accurate when n is big. 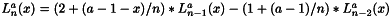$L_n^a(x) =(2+(a-1-x)/n)*L_{n-1}^a(x) - (1+(a-1)/n)*L_{n-2}^a(x)$ Also use pre-computed table Table[CoefficientList[LaguerreL[n, a, x], x], {n, 0, 10}] in mathematica.

Definition at line 752 of file utlMath.h.

References utlException.

Referenced by itk::SphericalPolarFourierRadialGenerator< PreciseType >::Evaluate().

Here is the caller graph for this function:

std::vector<double> utl::GetCoefLaguerreProduct	(	const int	n1,
		const double	a1,
		const int	n2,
		const double	a2
	)

inline

Get the coefficient vector of the product of $L_{n1}^{a1}(x)$ and $L_{n2}^{a2}(x)$

Definition at line 867 of file utlMath.h.

template<class T >

void utl::GetColumn	(	const vnl_matrix< T > &	mat,
		const int	index,
		vnl_vector< T > &	v1
	)

inline

Definition at line 238 of file utlVNLBlas.h.

Referenced by utl::NDArray< T, 2 >::GetColumn(), and utl::NDArray< T, 2 >::GetColumns().

Here is the caller graph for this function:

template<class T >

void utl::GetEqualityConstraintProjection	(	const vnl_matrix< T > &	Aeq,
		const vnl_vector< T > &	beq,
		const vnl_matrix< T > &	QInverse,
		vnl_matrix< T > &	projMatrix,
		vnl_vector< T > &	projVector
	)

The projection onto the plane Aeq^T*x=beq

Definition at line 374 of file utlVNLLapack.h.

References utl::PInverseSymmericVnlMatrix(), utl::ProductVnlMM(), utl::ProductVnlMv(), and utlException.

Here is the call graph for this function:

double utl::GetExpLegendreCoef	(	const double	a,
		const int	l,
		Func1To1	expF = `&std::exp`
	)

inline

Get the legendre coefficient vector of 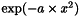$\exp(-a\times x^2)$ , i.e.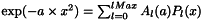 $\exp(-a\times x^2) = \sum_{l=0}^{lMax} A_l(a) P_l(x)$

Definition at line 919 of file utlMath.h.

Referenced by utl::GetExpProductLegendreCoef(), utl::GetSymmetricTensorSHCoef(), and utl::GetSymmetricTensorSHCoefDerivative().

Here is the caller graph for this function:

double utl::GetExpLegendreCoefDerivative	(	const double	a,
		const int	l,
		Func1To1	expF = `&std::exp`
	)

inline

Get the derivative 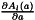$\frac{\partial A_l(a)}{\partial a}$ of the legendre coefficient vector of 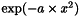$\exp(-a\times x^2)$ , i.e.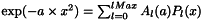 $\exp(-a\times x^2) = \sum_{l=0}^{lMax} A_l(a) P_l(x)$

Definition at line 1042 of file utlMath.h.

Referenced by utl::GetSymmetricTensorSHCoefDerivative().

Here is the caller graph for this function:

double utl::GetExpProductLegendreCoef	(	const double	a,
		const double	b,
		const int	l
	)

inline

Get the legendre coefficient vector of 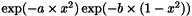$\exp(-a\times x^2)\exp(-b\times (1-x^2))$ , i.e. 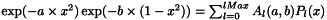$\exp(-a\times x^2)\exp(-b\times (1-x^2)) = \sum_{l=0}^{lMax} A_l(a,b) P_l(x)$ . In mathematica: (2*l + 1)/2* Integrate[ LegendreP[l, x]*Exp[-a1*x^2] Exp[-a2*(1 - x^2)], {x, -1, 1}]

Definition at line 243 of file itkSpecialFunctionGenerator.hxx.

References utl::GetExpLegendreCoef(), utl::IsInt(), and itk::lutExpValue().

Referenced by utl::ComputeDWISHCoefficientsForGPDCylinder().

Here is the call graph for this function:

Here is the caller graph for this function:

template<class T >

int utl::getrf	(	int	matrix_layout,
		int	m,
		int	n,
		T *	a,
		int	lda,
		int *	ipiv
	)

inline

template<>

int utl::getrf< double >	(	int	matrix_layout,
		int	m,
		int	n,
		double *	a,
		int	lda,
		int *	ipiv
	)

inline

Definition at line 295 of file utlLapack.h.

template<>

int utl::getrf< float >	(	int	matrix_layout,
		int	m,
		int	n,
		float *	a,
		int	lda,
		int *	ipiv
	)

inline

Definition at line 298 of file utlLapack.h.

template<>

int utl::getrf< std::complex< double > >	(	int	matrix_layout,
		int	m,
		int	n,
		std::complex< double > *	a,
		int	lda,
		int *	ipiv
	)

inline

Definition at line 301 of file utlLapack.h.

template<>

int utl::getrf< std::complex< float > >	(	int	matrix_layout,
		int	m,
		int	n,
		std::complex< float > *	a,
		int	lda,
		int *	ipiv
	)

inline

Definition at line 304 of file utlLapack.h.

template<class T >

int utl::getri	(	int	matrix_layout,
		int	n,
		T *	a,
		int	lda,
		const int *	ipiv
	)

inline

template<>

int utl::getri< double >	(	int	matrix_layout,
		int	n,
		double *	a,
		int	lda,
		const int *	ipiv
	)

inline

Definition at line 308 of file utlLapack.h.

template<>

int utl::getri< float >	(	int	matrix_layout,
		int	n,
		float *	a,
		int	lda,
		const int *	ipiv
	)

inline

Definition at line 311 of file utlLapack.h.

template<>

int utl::getri< std::complex< double > >	(	int	matrix_layout,
		int	n,
		std::complex< double > *	a,
		int	lda,
		const int *	ipiv
	)

inline

Definition at line 314 of file utlLapack.h.

template<>

int utl::getri< std::complex< float > >	(	int	matrix_layout,
		int	n,
		std::complex< float > *	a,
		int	lda,
		const int *	ipiv
	)

inline

Definition at line 317 of file utlLapack.h.

template<class T >

void utl::GetRow	(	const vnl_matrix< T > &	mat,
		const int	index,
		vnl_vector< T > &	v1
	)

inline

Definition at line 229 of file utlVNLBlas.h.

Referenced by utl::NDArray< T, 2 >::GetRow(), and utl::NDArray< T, 2 >::GetRows().

Here is the caller graph for this function:

template<class T >

utl_shared_ptr< utl::NDArray< T, 1 > > utl::GetSymmetricTensorSHCoef	(	const T	b,
		const T	e1,
		const T	e2,
		const int	lMax,
		const T	theta = `0`,
		const T	phi = `0`
	)

get the SH coefficients from the symmetric tensor with eigenvalues (e1,e2,e2), e1>e2, and (theta,phi) is the angular direction of the e1 axis.

Definition at line 180 of file itkSpecialFunctionGenerator.hxx.

References utl::GetExpLegendreCoef(), utl::GetIndexSHj(), utl::IsInt(), itk::lutExpValue(), M_PI, utl::RankToDimSH(), itk::SphericalHarmonicsGenerator< PreciseType >::RealSH(), utl::SQRTPI, and utlException.

Here is the call graph for this function:

template<class T >

std::vector< std::vector< T > > utl::GetSymmetricTensorSHCoefDerivative	(	const T	b,
		const T	e1,
		const T	e2,
		const int	lMax,
		const T	theta = `0`,
		const T	phi = `0`
	)

get the derivatives of the SH coefficients with respect to (e1, e2) in the symmetric tensor with eigenvalues (e1,e2,e2), e1>e2, and (theta,phi) is the angular direction of the e1 axis. The returned matrix is a CImg<T>(utl::rank2dimSH(lMax),2)

Definition at line 215 of file itkSpecialFunctionGenerator.hxx.

References utl::GetExpLegendreCoef(), utl::GetExpLegendreCoefDerivative(), utl::GetIndexSHj(), utl::IsInt(), itk::lutExpValue(), M_PI, utl::RankToDimSH(), itk::SphericalHarmonicsGenerator< PreciseType >::RealSH(), and utlException.

Here is the call graph for this function:

double utl::Hyperg1F1	(	double	a,
		double	b,
		double	x
	)

inline

Confluent hypergeometric function.

NOTE: std::tr1::conf_hyperg is better than gsl_sf_hyperg_1F1, considering gsl_sf_hyperg_1F1 has some potential underflow problems

Definition at line 40 of file itkSpecialFunctionGenerator.hxx.

Referenced by itk::SphericalPolarFourierRadialGenerator< PreciseType >::Evaluate().

Here is the caller graph for this function:

template<class T >

T utl::InnerProduct	(	const vnl_vector< T > &	v1,
		const vnl_vector< T > &	v2
	)

inline

Definition at line 189 of file utlVNLBlas.h.

References utlSAException.

template<class TVector1 , class TVector2 >

double utl::InnerProduct	(	const TVector1 &	v1,
		const TVector2 &	v2,
		const int	N1
	)

inline

Definition at line 1322 of file utlMath.h.

Referenced by utl::DotProduct(), utl::InnerProduct(), and utl::NDArrayBase< T, 4 >::PrintInfo().

Here is the caller graph for this function:

template<class TMatrixType >

void utl::InverseSmallMatrix	(	const TMatrixType &	mat,
		TMatrixType &	result,
		const int	row
	)

inline

Inverse a small matrix with (i,j) defined. The result should be allocated correctly.

Parameters

row	shoud be in [1,4].

Definition at line 1213 of file utlMath.h.

Referenced by utl::InverseMatrix().

Here is the caller graph for this function:

template<class T >

void utl::InverseSymmericVnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_matrix< T > &	result,
		const T	eps = `1e-8`
	)

inline

inverse of a symmetric matrix (non-singular). If the matrix is singular, it stop with an error. It is fast than PInverseVnlMatrix, but only works for non-singular matrix.

Definition at line 284 of file utlVNLLapack.h.

References utl::MatrixCopy(), and utlGlobalException.

Here is the call graph for this function:

template<class T >

T utl::Lagurre	(	const int	n,
		const double	a,
		const T	x
	)

lagurre polynomial 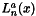$ L_n^a(x) $

Definition at line 52 of file itkSpecialFunctionGenerator.hxx.

Referenced by itk::ScalarMapFromSPFImageFilter< TInputImage, TOutputImage >::BeforeThreadedGenerateData(), and itk::SphericalPolarFourierRadialGenerator< PreciseType >::Evaluate().

Here is the caller graph for this function:

template<class T >

T utl::lange	(	int	matrix_order,
		char	norm,
		int	m,
		int	n,
		const T *	A,
		int	LDA
	)

inline

Referenced by utl::NDArray< T, 2 >::GetInfNorm(), and utl::NDArray< T, 2 >::GetOneNorm().

Here is the caller graph for this function:

double utl::lange	(	int	matrix_order,
		char	norm,
		int	m,
		int	n,
		const std::complex< double > *	A,
		int	LDA
	)

inline

Definition at line 288 of file utlLapack.h.

References LAPACKE_zlange().

Here is the call graph for this function:

float utl::lange	(	int	matrix_order,
		char	norm,
		int	m,
		int	n,
		const std::complex< float > *	A,
		int	LDA
	)

inline

Definition at line 291 of file utlLapack.h.

References LAPACKE_clange().

Here is the call graph for this function:

template<>

double utl::lange< double >	(	int	matrix_order,
		char	norm,
		int	m,
		int	n,
		const double *	A,
		int	LDA
	)

inline

Definition at line 282 of file utlLapack.h.

References LAPACKE_dlange().

Here is the call graph for this function:

template<>

float utl::lange< float >	(	int	matrix_order,
		char	norm,
		int	m,
		int	n,
		const float *	A,
		int	LDA
	)

inline

Definition at line 285 of file utlLapack.h.

References LAPACKE_slange().

Here is the call graph for this function:

float LAPACKE_clange	(	int	matrix_order,
		char	norm,
		lapack_int	m,
		lapack_int	n,
		const std::complex< float > *	a,
		lapack_int	lda
	)

Referenced by utl::lange().

Here is the caller graph for this function:

double LAPACKE_dlange	(	int	matrix_order,
		char	norm,
		lapack_int	m,
		lapack_int	n,
		const double *	a,
		lapack_int	lda
	)

Referenced by utl::lange< double >().

Here is the caller graph for this function:

float LAPACKE_slange	(	int	matrix_order,
		char	norm,
		lapack_int	m,
		lapack_int	n,
		const float *	a,
		lapack_int	lda
	)

Referenced by utl::lange< float >().

Here is the caller graph for this function:

double LAPACKE_zlange	(	int	matrix_order,
		char	norm,
		lapack_int	m,
		lapack_int	n,
		const std::complex< double > *	a,
		lapack_int	lda
	)

Referenced by utl::lange().

Here is the caller graph for this function:

double utl::LegendrePolynomialAt0 ( const int order )

inline

Definition at line 718 of file utlMath.h.

template<class ExprT >

auto utl::Log ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Log <typename ExprT::ValueType> >(expr))

Definition at line 359 of file utlFunctors.h.

Referenced by itk::DiffusionTensor< TPrecision >::GeodesicDistance(), and itk::DiffusionTensor< TPrecision >::LogEucDistance().

Here is the caller graph for this function:

template<class ExprT >

auto utl::Log10 ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Log10 <typename ExprT::ValueType> >(expr))

Definition at line 360 of file utlFunctors.h.

template<class ExprT >

auto utl::Log2 ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Log2 <typename ExprT::ValueType> >(expr))

Definition at line 361 of file utlFunctors.h.

template<class ExprT >

auto utl::LRound ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: LRound <typename ExprT::ValueType> >(expr))

Definition at line 365 of file utlFunctors.h.

template<class T >

void utl::MatrixCopy	(	const vnl_matrix< T > &	mat,
		vnl_matrix< T > &	matOut,
		const T	alpha,
		const char	trans = `'N'`
	)

inline

MatrixCopy. A := alpha * op(A)

Template Parameters

T

Parameters

mat	input matrix
matOut	output matrix
alpha	scale factor
trans	'N' or 'n': op(A) is A; 'T' or 't': op(A) is transpose of A; 'C' or 'c': conjugate transpose; 'R' or 'r': conjugate

Definition at line 45 of file utlVNLBlas.h.

References utl::cblas_copy(), and utlException.

Referenced by utl::gesdd_VnlMatrix(), utl::gesvd_VnlMatrix(), utl::InverseSymmericVnlMatrix(), utl::syev_VnlMatrix(), and utl::syevd_VnlMatrix().

Here is the call graph for this function:

Here is the caller graph for this function:

template<class TLeft , class TRight >

auto utl::Max	(	const TLeft &	lhs,
		const TRight &	rhs
	)		-> decltype(utl::F<utl::Functor:: Max <Expr2ValueType<TLeft,TRight>> >(lhs, rhs))

Definition at line 383 of file utlFunctors.h.

template<class TLeft >

auto utl::Max	(	const TLeft &	lhs,
		const ScalarExpr &	rhs
	)		-> decltype(utl::F<utl::Functor:: Max <Expr2ValueType<TLeft,ScalarExpr>> >(lhs, rhs))

Definition at line 383 of file utlFunctors.h.

template<class TRight >

auto utl::Max	(	const ScalarExpr &	lhs,
		const TRight &	rhs
	)		-> decltype(utl::F<utl::Functor:: Max <Expr2ValueType<ScalarExpr,TRight>> >(lhs, rhs))

Definition at line 383 of file utlFunctors.h.

template<class TRight >

auto utl::Min	(	const ScalarExpr &	lhs,
		const TRight &	rhs
	)		-> decltype(utl::F<utl::Functor:: Min <Expr2ValueType<ScalarExpr,TRight>> >(lhs, rhs))

Definition at line 384 of file utlFunctors.h.

template<class TLeft , class TRight >

auto utl::Min	(	const TLeft &	lhs,
		const TRight &	rhs
	)		-> decltype(utl::F<utl::Functor:: Min <Expr2ValueType<TLeft,TRight>> >(lhs, rhs))

Definition at line 384 of file utlFunctors.h.

template<class TLeft >

auto utl::Min	(	const TLeft &	lhs,
		const ScalarExpr &	rhs
	)		-> decltype(utl::F<utl::Functor:: Min <Expr2ValueType<TLeft,ScalarExpr>> >(lhs, rhs))

Definition at line 384 of file utlFunctors.h.

template<class T >

void utl::mkl_imatcopy	(	const char	ordering,
		const char	trans,
		const int	rows,
		const int	cols,
		const T	alpha,
		T *	A,
		const int	lda,
		const int	ldb
	)

inline

in-place copy or transpose

template<>

void utl::mkl_imatcopy< double >	(	const char	ordering,
		const char	trans,
		const int	rows,
		const int	cols,
		const double	alpha,
		double *	A,
		const int	lda,
		const int	ldb
	)

inline

Definition at line 44 of file utlMKL.h.

template<>

void utl::mkl_imatcopy< float >	(	const char	ordering,
		const char	trans,
		const int	rows,
		const int	cols,
		const float	alpha,
		float *	A,
		const int	lda,
		const int	ldb
	)

inline

Definition at line 49 of file utlMKL.h.

template<>

void utl::mkl_imatcopy< std::complex< double > >	(	const char	ordering,
		const char	trans,
		const int	rows,
		const int	cols,
		const std::complex< double >	alpha,
		std::complex< double > *	A,
		const int	lda,
		const int	ldb
	)

inline

Definition at line 54 of file utlMKL.h.

template<>

void utl::mkl_imatcopy< std::complex< float > >	(	const char	ordering,
		const char	trans,
		const int	rows,
		const int	cols,
		const std::complex< float >	alpha,
		std::complex< float > *	A,
		const int	lda,
		const int	ldb
	)

inline

Definition at line 59 of file utlMKL.h.

template<class T >

void utl::mkl_omatcopy	(	const char	ordering,
		const char	trans,
		const int	rows,
		const int	cols,
		const T	alpha,
		const T *	A,
		const int	lda,
		T *	B,
		const int	ldb
	)

inline

out-place copy or transpose

template<>

void utl::mkl_omatcopy< double >	(	const char	ordering,
		const char	trans,
		const int	rows,
		const int	cols,
		const double	alpha,
		const double *	A,
		const int	lda,
		double *	B,
		const int	ldb
	)

inline

Definition at line 65 of file utlMKL.h.

template<>

void utl::mkl_omatcopy< float >	(	const char	ordering,
		const char	trans,
		const int	rows,
		const int	cols,
		const float	alpha,
		const float *	A,
		const int	lda,
		float *	B,
		const int	ldb
	)

inline

Definition at line 70 of file utlMKL.h.

template<>

void utl::mkl_omatcopy< std::complex< double > >	(	const char	ordering,
		const char	trans,
		const int	rows,
		const int	cols,
		const std::complex< double >	alpha,
		const std::complex< double > *	A,
		const int	lda,
		std::complex< double > *	B,
		const int	ldb
	)

inline

Definition at line 75 of file utlMKL.h.

template<>

void utl::mkl_omatcopy< std::complex< float > >	(	const char	ordering,
		const char	trans,
		const int	rows,
		const int	cols,
		const std::complex< float >	alpha,
		const std::complex< float > *	A,
		const int	lda,
		std::complex< float > *	B,
		const int	ldb
	)

inline

Definition at line 80 of file utlMKL.h.

template<class ExprT >

auto utl::Neg ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Neg <typename ExprT::ValueType> >(expr))

Definition at line 366 of file utlFunctors.h.

template<class T >

void utl::OuterProduct	(	const vnl_vector< T > &	v1,
		const vnl_vector< T > &	v2,
		vnl_matrix< T > &	mat,
		const double	alpha = `1.0`
	)

inline

$ A = alpha*x*y'+ A $

Definition at line 198 of file utlVNLBlas.h.

References CblasRowMajor.

template<class T >

void utl::OuterProduct	(	const vnl_vector< T > &	v1,
		vnl_matrix< T > &	mat,
		const double	alpha = `1.0`
	)

inline

$ A = alpha*x*x'+ A $

Definition at line 212 of file utlVNLBlas.h.

References CblasRowMajor, and CblasUpper.

template<class TVector1 , class TVector2 , class TMatrix >

void utl::OuterProduct	(	const TVector1 &	v1,
		const int	N1,
		const TVector2 &	v2,
		const int	N2,
		TMatrix &	mat
	)

inline

Outer project of two vectors. mat needs to be pre-allocated.

Definition at line 1299 of file utlMath.h.

Referenced by utl::MeanDirector().

Here is the caller graph for this function:

template<class TVector1 , class TMatrix >

void utl::OuterProduct	(	const TVector1 &	v1,
		const int	N1,
		TMatrix &	mat
	)

inline

Outer product of a product and itself.

Definition at line 1309 of file utlMath.h.

template<class T >

void utl::PInverseSymmericVnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_matrix< T > &	result,
		const T	eps = `1e-8`
	)

inline

pseudo-inverse of a symmetric matrix which can be singular. If the matrix is not singular, it returns the inverse.

Definition at line 321 of file utlVNLLapack.h.

References utl::EigenDecompositionSymmetricVnlMatrix(), utl::ProductVnlMM(), and utl::ProductVnlMtM().

Referenced by utl::GetEqualityConstraintProjection().

Here is the call graph for this function:

Here is the caller graph for this function:

template<class T >

void utl::PInverseVnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_matrix< T > &	result,
		const T	eps = `1e-8`
	)

inline

pseudo-inverse of a general matrix.

Definition at line 340 of file utlVNLLapack.h.

References utl::ProductVnlMM(), utl::ProductVnlMMt(), and utl::SVDVnlMatrix().

Here is the call graph for this function:

std::vector<std::complex<double> > utl::PolynomialRoot ( const std::vector< double > & coef )

inline

Get the analytic root of polynomial with order no more than 4. In mathematica: Solve[a3 x^3 + a2 x^2 + a1 x + a0 == 0, x]

Definition at line 1100 of file utlMath.h.

Referenced by itk::DiffusionTensor< TPrecision >::GetEigenValuesVectorsAnalytic().

Here is the caller graph for this function:

template<class TLeft >

auto utl::Pow	(	const TLeft &	lhs,
		const ScalarExpr &	rhs
	)		-> decltype(utl::F<utl::Functor:: Pow <Expr2ValueType<TLeft,ScalarExpr>> >(lhs, rhs))

Definition at line 385 of file utlFunctors.h.

template<class TLeft , class TRight >

auto utl::Pow	(	const TLeft &	lhs,
		const TRight &	rhs
	)		-> decltype(utl::F<utl::Functor:: Pow <Expr2ValueType<TLeft,TRight>> >(lhs, rhs))

Definition at line 385 of file utlFunctors.h.

Referenced by itk::DiffusionTensor< TPrecision >::InvSqrt(), itk::Functor::SHCoefficientsFit< T >::operator()(), and itk::DiffusionTensor< TPrecision >::Sqrt().

Here is the caller graph for this function:

template<class TRight >

auto utl::Pow	(	const ScalarExpr &	lhs,
		const TRight &	rhs
	)		-> decltype(utl::F<utl::Functor:: Pow <Expr2ValueType<ScalarExpr,TRight>> >(lhs, rhs))

Definition at line 385 of file utlFunctors.h.

double utl::PowHalfInteger	(	const double	a,
		const double	b
	)

inline

efficient way to calculate std::pow(a,b) when b is integer or half integer

Definition at line 170 of file utlMath.h.

References utl::IsInt(), utl::PowInteger(), and utlException.

Referenced by itk::SphericalPolarFourierRadialGenerator< PreciseType >::Evaluate(), and itk::SphericalPolarFourierRadialGenerator< PreciseType >::GetNormalizeFacotr().

Here is the call graph for this function:

Here is the caller graph for this function:

double utl::PowInteger	(	const double	a,
		const int	b
	)

inline

Definition at line 154 of file utlMath.h.

Referenced by utl::PowHalfInteger().

Here is the caller graph for this function:

template<class TMatrix1 , class TMatrix2 , class TMatrix3 >

void utl::ProductMM	(	const TMatrix1 &	mat1,
		int	rows,
		int	cols,
		const TMatrix2 &	mat2,
		int	cols2,
		TMatrix3 &	mat3
	)

inline

matrix matrix product. Direct calculation, efficient for small 3x3 matrices.

Definition at line 1386 of file utlMath.h.

template<class TMatrix , class TVector1 , class TVector2 >

void utl::ProductMv	(	const TMatrix &	mat,
		int	rows,
		int	cols,
		const TVector1 &	v1,
		TVector2 &	v2
	)

inline

matrix vector product. Direct calculation, efficient for small 3x3 matrices.

Definition at line 1360 of file utlMath.h.

template<class TVector1 , class TMatrix , class TVector2 >

void utl::ProductvM	(	const TVector1 &	v1,
		int	rows,
		const TMatrix &	mat,
		int	cols,
		TVector2 &	v2
	)

inline

vector matrix product. Direct calculation, efficient for small 3x3 matrices.

Definition at line 1373 of file utlMath.h.

template<class T >

void utl::ProductVnlMM	(	const vnl_matrix< T > &	A,
		const vnl_matrix< T > &	B,
		vnl_matrix< T > &	C,
		const double	alpha = `1.0`,
		const double	beta = `0.0`
	)

inline

Definition at line 117 of file utlVNLBlas.h.

Referenced by utl::GetEqualityConstraintProjection(), utl::PInverseSymmericVnlMatrix(), and utl::PInverseVnlMatrix().

Here is the caller graph for this function:

template<class T >

void utl::ProductVnlMM	(	const vnl_matrix< T > &	A1,
		const vnl_matrix< T > &	A2,
		const vnl_matrix< T > &	A3,
		vnl_matrix< T > &	C
	)

inline

Definition at line 117 of file utlVNLBlas.h.

template<class T >

void utl::ProductVnlMM	(	const vnl_matrix< T > &	A1,
		const vnl_matrix< T > &	A2,
		const vnl_matrix< T > &	A3,
		const vnl_matrix< T > &	A4,
		const vnl_matrix< T > &	A5,
		vnl_matrix< T > &	C
	)

inline

Definition at line 117 of file utlVNLBlas.h.

template<class T >

void utl::ProductVnlMM	(	const vnl_matrix< T > &	A1,
		const vnl_matrix< T > &	A2,
		const vnl_matrix< T > &	A3,
		const vnl_matrix< T > &	A4,
		vnl_matrix< T > &	C
	)

inline

Definition at line 117 of file utlVNLBlas.h.

template<class T >

void utl::ProductVnlMMt	(	const vnl_matrix< T > &	A,
		const vnl_matrix< T > &	B,
		vnl_matrix< T > &	C,
		const double	alpha = `1.0`,
		const double	beta = `0.0`
	)

inline

Definition at line 117 of file utlVNLBlas.h.

Referenced by utl::PInverseVnlMatrix().

Here is the caller graph for this function:

template<class T >

void utl::ProductVnlMtM	(	const vnl_matrix< T > &	A,
		const vnl_matrix< T > &	B,
		vnl_matrix< T > &	C,
		const double	alpha = `1.0`,
		const double	beta = `0.0`
	)

inline

Definition at line 117 of file utlVNLBlas.h.

Referenced by utl::PInverseSymmericVnlMatrix().

Here is the caller graph for this function:

template<class T >

void utl::ProductVnlMtMt	(	const vnl_matrix< T > &	A,
		const vnl_matrix< T > &	B,
		vnl_matrix< T > &	C,
		const double	alpha = `1.0`,
		const double	beta = `0.0`
	)

inline

Definition at line 117 of file utlVNLBlas.h.

template<class T >

void utl::ProductVnlMtv	(	const vnl_matrix< T > &	A,
		const vnl_vector< T > &	b,
		vnl_vector< T > &	c,
		const double	alpha = `1.0`,
		const double	beta = `0.0`
	)

inline

Definition at line 140 of file utlVNLBlas.h.

template<class T >

void utl::ProductVnlMv	(	const vnl_matrix< T > &	A,
		const vnl_vector< T > &	b,
		vnl_vector< T > &	c,
		const double	alpha = `1.0`,
		const double	beta = `0.0`
	)

inline

Definition at line 140 of file utlVNLBlas.h.

Referenced by utl::GetEqualityConstraintProjection().

Here is the caller graph for this function:

template<class T >

void utl::ProductVnlvM	(	const vnl_vector< T > &	b,
		const vnl_matrix< T > &	A,
		vnl_vector< T > &	c,
		const double	alpha = `1.0`,
		const double	beta = `0.0`
	)

inline

Definition at line 161 of file utlVNLBlas.h.

template<class T >

void utl::ProductVnlvMt	(	const vnl_vector< T > &	b,
		const vnl_matrix< T > &	A,
		vnl_vector< T > &	c,
		const double	alpha = `1.0`,
		const double	beta = `0.0`
	)

inline

Definition at line 161 of file utlVNLBlas.h.

template<class T >

void utl::ProductVnlXtX	(	const vnl_matrix< T > &	A,
		vnl_matrix< T > &	C,
		const double	alpha = `1.0`,
		const double	beta = `0.0`
	)

Definition at line 185 of file utlVNLBlas.h.

template<class T >

void utl::ProductVnlXXt	(	const vnl_matrix< T > &	A,
		vnl_matrix< T > &	C,
		const double	alpha = `1.0`,
		const double	beta = `0.0`
	)

Definition at line 185 of file utlVNLBlas.h.

template<class VectorType , class MatrixType >

void utl::RotationMatrixFromUnitNormVectors	(	const VectorType &	from,
		const VectorType &	to,
		MatrixType &	mtx
	)

A function for creating a rotation matrix that rotates a vector called "from" into another vector called "to". Input : from[3], to[3] which both must be normalized non-zero vectors Output: mtx[3][3] – a 3x3 matrix in colum-major form Authors: Tomas Moller, John Hughes "Efficiently Building a Matrix to Rotate One Vector to Another" Journal of Graphics Tools, 4(4):1-4, 1999

Definition at line 37 of file utlRotationMatrixFromVectors.h.

template<class VectorType , class MatrixType >

void utl::RotationMatrixFromVectors	(	const VectorType &	from,
		const VectorType &	to,
		MatrixType &	mat
	)

this function accepts vectors with arbitrary norm

Definition at line 130 of file utlRotationMatrixFromVectors.h.

References spams::abs(), and utlException.

Referenced by utl::ComputeOrientationalOrderFromSHCoefficients().

Here is the call graph for this function:

Here is the caller graph for this function:

template<class ExprT >

auto utl::Round ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Round <typename ExprT::ValueType> >(expr))

Definition at line 364 of file utlFunctors.h.

template<class ExprT >

auto utl::Sign ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Sign <typename ExprT::ValueType> >(expr))

Definition at line 367 of file utlFunctors.h.

template<class ExprT >

auto utl::Sin ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Sin <typename ExprT::ValueType> >(expr))

Definition at line 371 of file utlFunctors.h.

template<class ExprT >

auto utl::Sqrt ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Sqrt <typename ExprT::ValueType> >(expr))

Definition at line 362 of file utlFunctors.h.

Referenced by spams::Matrix< T >::fakeSize(), and spams::Vector< int >::setn().

Here is the caller graph for this function:

template<class ExprT >

auto utl::Square ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Square <typename ExprT::ValueType> >(expr))

Definition at line 368 of file utlFunctors.h.

template<class TVector1 >

double utl::SquaredTwoNorm	(	const TVector1 &	v1,
		const int	N1
	)

inline

Definition at line 1339 of file utlMath.h.

template<class T >

void utl::SVDVnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_matrix< T > &	U,
		vnl_vector< T > &	s,
		vnl_matrix< T > &	V,
		char	format = `'S'`
	)

inline

SVDVnlMatrix.

Parameters

mat	matrix with size MxN.
U	left singular vectors. If format is 'A', U is MxM matrix. If format is 'S', U size is M x min(M,N)
s	singular values with size min(M,N). Sored in decreasing order.
V	right singular vectors. If format is 'A', V size is NxN. If format is 'S', V size is N x min(M,N)
format	'S' or 'A'. 'A' means full size, 'S' means reduced size.

Definition at line 270 of file utlVNLLapack.h.

Referenced by utl::PInverseVnlMatrix().

Here is the caller graph for this function:

template<class T >

int utl::syev	(	int	matrix_order,
		char	JOBZ,
		char	UPLO,
		int	N,
		T *	A,
		int	LDA,
		T *	W
	)

inline

template function definitions

template<>

int utl::syev< double >	(	int	matrix_order,
		char	JOBZ,
		char	UPLO,
		int	N,
		double *	A,
		int	LDA,
		double *	W
	)

inline

function implementations using double and float

Definition at line 200 of file utlLapack.h.

template<>

int utl::syev< float >	(	int	matrix_order,
		char	JOBZ,
		char	UPLO,
		int	N,
		float *	A,
		int	LDA,
		float *	W
	)

inline

Definition at line 203 of file utlLapack.h.

template<class T >

void utl::syev_VnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_vector< T > &	eigenValues,
		vnl_matrix< T > &	eigenVectors
	)

inline

syev_VnlMatrix eigen-decomposition for symmetric matrix. http://www.netlib.org/lapack/explore-html/dd/d4c/dsyev_8f.html

Parameters

mat	a symmetric matrix (only upper triangular matrix is used)
eigenValues	Eigen-values are in increasing order.
eigenVectors	Eigen-vectors. each row is an eigen-vector

Definition at line 71 of file utlVNLLapack.h.

References utl::MatrixCopy(), utlException, and utlGlobalException.

Here is the call graph for this function:

template<class T >

int utl::syevd	(	int	matrix_order,
		char	JOBZ,
		char	UPLO,
		int	N,
		T *	A,
		int	LDA,
		T *	W
	)

inline

template<>

int utl::syevd< double >	(	int	matrix_order,
		char	JOBZ,
		char	UPLO,
		int	N,
		double *	A,
		int	LDA,
		double *	W
	)

inline

Definition at line 207 of file utlLapack.h.

template<>

int utl::syevd< float >	(	int	matrix_order,
		char	JOBZ,
		char	UPLO,
		int	N,
		float *	A,
		int	LDA,
		float *	W
	)

inline

Definition at line 210 of file utlLapack.h.

template<>

int utl::syevd< std::complex< double > >	(	int	matrix_order,
		char	JOBZ,
		char	UPLO,
		int	N,
		std::complex< double > *	A,
		int	LDA,
		std::complex< double > *	W
	)

inline

Definition at line 213 of file utlLapack.h.

References utlGlobalException.

template<>

int utl::syevd< std::complex< float > >	(	int	matrix_order,
		char	JOBZ,
		char	UPLO,
		int	N,
		std::complex< float > *	A,
		int	LDA,
		std::complex< float > *	W
	)

inline

Definition at line 216 of file utlLapack.h.

References utlGlobalException.

template<class T >

void utl::syevd_VnlMatrix	(	const vnl_matrix< T > &	mat,
		vnl_vector< T > &	eigenValues,
		vnl_matrix< T > &	eigenVectors
	)

inline

syevd_VnlMatrix eigen-decomposition for symmetric matrix. dsyevd is faster than dsyev http://www.netlib.org/lapack/explore-html/d1/da2/dsyevd_8f.html

Parameters

mat	a symmetric matrix (only upper triangular matrix is used)
eigenValues	Eigen-values are in increasing order.
eigenVectors	Eigen-vectors. each row is an eigen-vector

Definition at line 103 of file utlVNLLapack.h.

References utl::MatrixCopy(), utlException, and utlGlobalException.

Here is the call graph for this function:

template<class T >

void utl::syrk_VnlMatrix	(	const bool	trans,
		const T	alpha,
		const vnl_matrix< T > &	A,
		const T	beta,
		vnl_matrix< T > &	C
	)

inline

syrk_VnlMatrix

define several functions.

Parameters

trans	If false, then C := alpha* AA' + beta C; If true, then C := alpha* A'A + beta C
alpha
A	MxN matrix
beta
C	MxM or NxN symmetric matrix

template <class T> inline void syrk_VnlMatrix( const bool trans, const T alpha, const vnl_matrix<T>& A, const T beta, vnl_matrix<T>& C )

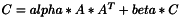
$ C = alpha *A*A^T + beta*C $
template <class T> void ProductVnlXXt ( const vnl_matrix<T>& A, vnl_matrix<T>& C, const double alpha=1.0, const double beta=0.0 )

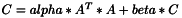
$ C = alpha *A^T*A + beta*C $
template <class T> void ProductVnlXtX ( const vnl_matrix<T>& A, vnl_matrix<T>& C, const double alpha=1.0, const double beta=0.0 )

Definition at line 185 of file utlVNLBlas.h.

template<class T >

int utl::sytrf	(	int	matrix_order,
		char	UPLO,
		int	N,
		T *	A,
		int	LDA,
		int *	IPIV
	)

inline

template<>

int utl::sytrf< double >	(	int	matrix_order,
		char	UPLO,
		int	N,
		double *	A,
		int	LDA,
		int *	IPIV
	)

inline

Definition at line 269 of file utlLapack.h.

template<>

int utl::sytrf< float >	(	int	matrix_order,
		char	UPLO,
		int	N,
		float *	A,
		int	LDA,
		int *	IPIV
	)

inline

Definition at line 272 of file utlLapack.h.

template<>

int utl::sytrf< std::complex< double > >	(	int	matrix_order,
		char	UPLO,
		int	N,
		std::complex< double > *	A,
		int	LDA,
		int *	IPIV
	)

inline

Definition at line 275 of file utlLapack.h.

template<>

int utl::sytrf< std::complex< float > >	(	int	matrix_order,
		char	UPLO,
		int	N,
		std::complex< float > *	A,
		int	LDA,
		int *	IPIV
	)

inline

Definition at line 278 of file utlLapack.h.

template<class T >

int utl::sytri	(	int	matrix_order,
		char	UPLO,
		int	N,
		T *	A,
		int	LDA,
		const int *	IPIV
	)

inline

template<>

int utl::sytri< double >	(	int	matrix_order,
		char	UPLO,
		int	N,
		double *	A,
		int	LDA,
		const int *	IPIV
	)

inline

Definition at line 256 of file utlLapack.h.

template<>

int utl::sytri< float >	(	int	matrix_order,
		char	UPLO,
		int	N,
		float *	A,
		int	LDA,
		const int *	IPIV
	)

inline

Definition at line 259 of file utlLapack.h.

template<>

int utl::sytri< std::complex< double > >	(	int	matrix_order,
		char	UPLO,
		int	N,
		std::complex< double > *	A,
		int	LDA,
		const int *	IPIV
	)

inline

Definition at line 262 of file utlLapack.h.

template<>

int utl::sytri< std::complex< float > >	(	int	matrix_order,
		char	UPLO,
		int	N,
		std::complex< float > *	A,
		int	LDA,
		const int *	IPIV
	)

inline

Definition at line 265 of file utlLapack.h.

template<class ExprT >

auto utl::Tan ( const ExprT & expr ) -> decltype(utl::F<utl::Functor:: Tan <typename ExprT::ValueType> >(expr))

Definition at line 373 of file utlFunctors.h.

double utl::w_im ( double x )

inline

Compute w(z) = exp(-z^2) erfc(-iz) [ Faddeeva / scaled complex error func ] Special-case code for Im[w(x)] of real x.

Definition at line 656 of file utlMath.h.

References utl::w_im_y100().

Referenced by utl::Erfi().

Here is the call graph for this function:

Here is the caller graph for this function:

static double utl::w_im_y100	(	double	y100,
		double	x
	)

static

Definition at line 247 of file utlMath.h.

Referenced by utl::DawsonF(), and utl::w_im().

Here is the caller graph for this function:

Variable Documentation

const double utl::BesselJPrimeZerosOrder1[60]

static

Initial value:

= 
  {
841183781340659, 5.331442773525033, 8.536316366346325, 11.706004902592063, 14.863588633909032, 18.015527862681804, 21.164369859188792, 
311326857210776, 27.457050571059245, 30.601922972669094, 33.746182898667385, 36.88998740923681, 40.03344405335068, 43.17662896544882, 
319597561173914, 49.46239113970275, 52.60504111155669, 55.74757179225101, 58.8900022991857, 62.03234787066199, 65.17462080254445, 
31683112595181, 71.458987105851, 74.60109561345641, 77.74316240819677, 80.88519235387844, 84.02718958629353, 87.16915764454028, 
31109957490342, 93.45301801376003, 96.59491525429114, 99.73679330057391, 102.87865391175445, 106.0204986383608, 109.16232885234086, 
30414577205505, 115.44595048318557, 118.58774395631993, 121.7295270618102, 124.87130058238789, 128.01306522392028, 131.15482162462013, 
29657036296211, 137.43831196451296, 140.58004690784534, 143.72177562967596, 146.86349852934376, 150.0052159727252, 153.14692829566764, 
28863580700812, 159.43033879123553, 162.57203751084367, 165.71373220841684, 168.85542310848228, 171.99711041915972, 175.13879433363329, 
28047503146777, 181.42215267978807, 184.56382743433812, 187.70549944043358
  }

BesselJPrimeZeros in Mathematica, the first 60 solutions of J'_1(x)=0.

Definition at line 66 of file utlMath.h.

Referenced by utl::ComputeDWISHCoefficientsForGPDCylinder().

const double utl::BesselJPrimeZerosTable[]

static

Initial value:

= 
  {
   
0,3.8317059702075125,7.0155866698156055,10.173468135062722,13.323691936314223,16.47063005087763,19.615858510468243,22.760084380592772,25.903672087618382,29.046828534916855,           
   
841183781340659,5.3314427735250325,8.536316366346284,11.706004902592063,14.863588633909034,18.015527862681804,21.16436985918879,24.311326857210776,27.457050571059245,30.601922972669094,
   
0542369282271404,6.706133194158457,9.969467823087596,13.170370856016122,16.347522318321783,19.512912782488204,22.671581772477424,25.826037141785264,28.977672772993678,32.127327020443474,
   
201188941210528,8.015236598375951,11.345924310742964,14.585848286167028,17.78874786606647,20.9724769365377,24.144897432909264,27.310057930204348,30.470268806290424,33.62694918279668,
   
317553126083994,9.282396285241617,12.68190844263889,15.964107037731551,19.196028800048904,22.401032267689004,25.589759681386735,28.767836217666503,31.938539340972785,35.10391667734677,
   
41561637570024,10.519860873772291,13.9871886301403,17.312842487884627,20.57551452138689,23.803581476593862,27.01030789777772,30.20284907898166,33.38544390101012,36.56077768688036,
   
5012661446841475,11.734935953042752,15.268181461097873,18.637443009666203,21.931715017802237,25.183925599499627,28.409776362510083,31.617875716105036,34.81339298429743,37.9996408977153,
   
57783648971416,12.93238623709143,16.529365884366943,19.941853366527344,23.26805292645757,26.545032061823576,29.790748583196613,33.015178641375144,36.22438054878716,39.42227457893926,
   
647421651997242,14.11551890789478,17.774012366915255,21.229062622853125,24.58719748631768,27.889269427955092,31.155326556188324,34.396628554272176,37.620078044197086,40.83017868182204,
   
711433970699948,15.286737667333524,19.004593537946054,22.501398726777285,25.891277276839137,29.21856349993608,32.50524735237553,35.7637929288088,39.00190281151422,42.22463843075328,
   
770876674955586,16.447852748486536,20.223031412681703,23.760715860327448,27.182021527190532,30.534504754007074,33.84196577513571,37.118000423665606,40.37106890533389,43.60676490137951,
  }

BesselJPrimeZeros in Mathematica, the k-th solution of J'_m(x)=0

Definition at line 37 of file utlMath.h.

Referenced by itk::CylinderModelGenerator< PreciseType >::ComputeDWISamples().

constexpr double utl::E = 2.71828182845904523536028747135

static

E

Definition at line 25 of file utlConstants.h.

Referenced by spams::coreSOMP(), spams::Vector< T >::std(), and spams::FISTA::Loss< T, Matrix< T >, Matrix< T > >::~Loss().

const unsigned long utl::FactorialTable[21]

static

Initial value:

=
  {
  1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 
  39916800, 479001600, 6227020800, 87178291200, 1307674368000, 20922789888000, 
  355687428096000, 6402373705728000, 121645100408832000,2432902008176640000
  
  }

pre-computed table for factorial of integers. Table[n!, {n, 0, 30}] in mathematica

Definition at line 117 of file utlMath.h.

const double utl::GammaHalfIntegerTable[30]

static

pre-computed table for Gamma[1/2], Gamma[3/2], etc. Table[N[Gamma[n/2], 35], {n, 1, 60, 2}] in mathematica.

Definition at line 81 of file utlMath.h.

constexpr double utl::LOG10E = 0.43429448190325182765112891892

static

log_10 (e)

Definition at line 29 of file utlConstants.h.

constexpr double utl::LOG2E = 1.44269504088896340735992468100

static

log_2 (e)

Definition at line 27 of file utlConstants.h.

constexpr double utl::PI = 3.14159265358979323846264338328

static

Pi

Definition at line 23 of file utlConstants.h.

constexpr double utl::PI_2 = 1.57079632679489661923132169164

static

Pi/2

Definition at line 37 of file utlConstants.h.

constexpr double utl::PI_4 = 0.78539816339744830961566084582

static

Pi/4

Definition at line 39 of file utlConstants.h.

constexpr double utl::SQRT1_2 = 0.70710678118654752440084436210

static

sqrt(1/2)

Definition at line 33 of file utlConstants.h.

Referenced by utl::Convert2To4Tensor(), and utl::ConvertTensor6DTo9D().

constexpr double utl::SQRT2 = 1.41421356237309504880168872421

static

sqrt(2)

Definition at line 31 of file utlConstants.h.

Referenced by utl::Convert4To2Tensor(), utl::ConvertTensor9DTo6D(), utl::GetE1E2FromFAMD(), itk::SphericalHarmonicsGenerator< PreciseType >::RealDerivativeOfPhi(), itk::SphericalHarmonicsGenerator< PreciseType >::RealDerivativeOfTheta(), itk::SphericalHarmonicsGenerator< PreciseType >::RealSH(), and itk::SphericalHarmonicsGenerator< PreciseType >::RealTripleIntegration().

constexpr double utl::SQRT3 = 1.73205080756887729352744634151

static

sqrt(3)

Definition at line 35 of file utlConstants.h.

constexpr double utl::SQRTPI = 1.77245385090551602729816748334

static

sqrt(Pi)

Definition at line 41 of file utlConstants.h.

Referenced by utl::ComputeDWISHCoefficientsForGPDCylinder(), utl::DawsonF(), and utl::GetSymmetricTensorSHCoef().

Namespaces

Macros

Typedefs

Functions

Variables

Detailed Description

Macro Definition Documentation

Typedef Documentation

Function Documentation

Variable Documentation